Identifying Species Network Features from Gene Tree Quartets Under the Coalescent Model
- PMID: 30094772
- PMCID: PMC6344282
- DOI: 10.1007/s11538-018-0485-4
Identifying Species Network Features from Gene Tree Quartets Under the Coalescent Model
Abstract
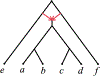
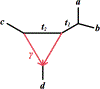
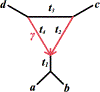
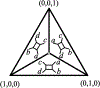
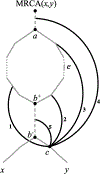
We show that many topological features of level-1 species networks are identifiable from the distribution of the gene tree quartets under the network multi-species coalescent model. In particular, every cycle of size at least 4 and every hybrid node in a cycle of size at least 5 are identifiable. This is a step toward justifying the inference of such networks which was recently implemented by Solís-Lemus and Ané. We show additionally how to compute quartet concordance factors for a network in terms of simpler networks, and explore some circumstances in which cycles of size 3 and hybrid nodes in 4-cycles can be detected.
Keywords: Coalescent theory; Concordance factors; Networks; Phylogenetics.
Figures
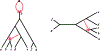






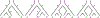
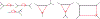

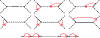
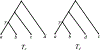
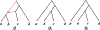


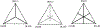


References
-
- Allman Elizabeth S., Degnan James H., and Rhodes John A.. Identifying the rooted species tree from the distribution of unrooted gene trees under the coalescent. Journal of Mathematical Biology, 62(6):833–862, 2011. - PubMed
-
- Ané Cécile, Larget Bret, Baum David A., Smith Stacey D., and Rokas Antonis. Bayesian estimation of concordance among gene trees. Molecular Biology and Evolution, 24(2):412–426, 2007. - PubMed
-
- Arnold Michael L.. Natural hybridization and evolution, volume 53 Oxford University Press, 1997.
-
- Bapteste Eric, van Iersel Leo, Janke Axel, Kelchner Scot, Kelk Steven, McInerney James O., Morrison David A., Nakhleh Luay, Steel Mike, Stougie Leen, and Whitfield James. Networks: expanding evolutionary thinking. Trends in Genetics, 29(8):439–441, 2013. - PubMed
-
- Carstens Bryan C., Lacey Knowles L, and Collins Tim. Estimating Species Phylogeny from Gene-Tree Probabilities Despite Incomplete Lineage Sorting: An Example from Melanoplus Grasshoppers. Systematic Biology, 56(3):400–411, 2007. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

