Regularization strategies in statistical image reconstruction of low-dose x-ray CT: A review

Abstract

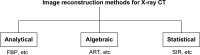
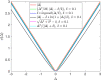
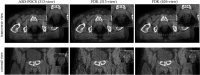
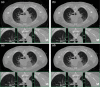
Statistical image reconstruction (SIR) methods have shown potential to substantially improve the image quality of low-dose x-ray computed tomography (CT) as compared to the conventional filtered back-projection (FBP) method. According to the maximum a posteriori (MAP) estimation, the SIR methods are typically formulated by an objective function consisting of two terms: (a) a data-fidelity term that models imaging geometry and physical detection processes in projection data acquisition, and (b) a regularization term that reflects prior knowledge or expectations of the characteristics of the to-be-reconstructed image. SIR desires accurate system modeling of data acquisition, while the regularization term also has a strong influence on the quality of reconstructed images. A variety of regularization strategies have been proposed for SIR in the past decades, based on different assumptions, models, and prior knowledge. In this paper, we review the conceptual and mathematical bases of these regularization strategies and briefly illustrate their efficacies in SIR of low-dose CT.

Keywords: low dose; regularization; statistical image reconstruction; x-ray CT.

Figure 1

List of image reconstruction methods for x‐ray CT.

Figure 2

Overview of the regularization strategies in SIR for low‐dose CT.

Figure 3

Plot of commonly used nonconvex potential functions.

Figure 4

Plot of commonly used convex potential functions.

Figure 5

Plot of convex potential functions corresponding to the q‐GGMRF priors.

Figure 6

Plot of the absolute value function and its differentiable approximations.

Figure 7

SIR reconstructions of a GE performance phantom by using: (a) GMRF prior p = 2, q = 2; (b) q‐GGMRF prior p = 2, q = 1.2; (c) GGMRF prior p = 1.1, q = 1.1. (Figure reprinted from Thibault et al. 2007, A three‐dimensional statistical approach to improved image quality for multislice helical CT, Med. Phys., 34: 4526–4544).

Figure 8

ASD‐POCS and FDK reconstructions of a prostate cancer patient in a clinical study. (Figure reprinted from Han et al., Algorithm‐enabled exploration of the image quality potential of cone beam CT in image‐guided radiation therapy, Phys. Med. Biol., 60: 4601–4633).

Figure 9

Plot of the sgn | (Δ) |  function and its asymptotic approximations.

Figure 10

A reconstructed slice of the patient from 120kVp, 20mAs acquisition: (a) FBP reconstruction; (b) SIR‐GMRF reconstruction; (c) SIR‐NLM reconstruction; (d) SIR‐adaptiveNLM reconstruction. (Figure reprinted from Zhang et al., Statistical image reconstruction for low‐dose CT using nonlocal means‐based regularization. Part II: An adaptive approach, Computerized Medical Imaging and Graphics, 43: 26‐35).

Figure 11

A reconstructed slice of a cardiac perfusion CT study from 440 projection views: (a) FBP; (b) SIR‐TV; (c) SIR‐GD; (d) SIR‐AD. (Figure reprinted from Xu et al., Low‐dose x‐ray CT reconstruction via dictionary learning, IEEE Trans. Med. Imag., 31(9): 1682‐1697).

Figure 12

Reconstruction of a cadaver by FBP, PL, rigid PIRPLE, and deformable PIRPLE with 20 projections and 1.25 mAs/projection. (Figure reprinted from Dang et al., dPIRPLE: a joint estimation framework for deformable registration and penalized‐likelihood CT image reconstruction using prior images, Phys. Med. Biol., 59: 4799–4826).