Synergistic Integration of Laboratory and Numerical Approaches in Studies of the Biomechanics of Diseased Red Blood Cells
- PMID: 30103419
- PMCID: PMC6164935
- DOI: 10.3390/bios8030076
Synergistic Integration of Laboratory and Numerical Approaches in Studies of the Biomechanics of Diseased Red Blood Cells
Abstract
In red blood cell (RBC) disorders, such as sickle cell disease, hereditary spherocytosis, and diabetes, alterations to the size and shape of RBCs due to either mutations of RBC proteins or changes to the extracellular environment, lead to compromised cell deformability, impaired cell stability, and increased propensity to aggregate. Numerous laboratory approaches have been implemented to elucidate the pathogenesis of RBC disorders. Concurrently, computational RBC models have been developed to simulate the dynamics of RBCs under physiological and pathological conditions. In this work, we review recent laboratory and computational studies of disordered RBCs. Distinguished from previous reviews, we emphasize how experimental techniques and computational modeling can be synergically integrated to improve the understanding of the pathophysiology of hematological disorders.
Keywords: laboratory approaches; numerical modeling; red blood cell disorders.
Conflict of interest statement
The authors declare no conflict of interest.
Figures




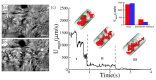


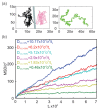
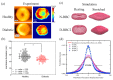
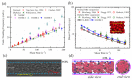
References
-
- Boal D.H. Mechanics of the Cell. Cambridge University Press; Cambridge, UK: 2012.
-
- Cooper G.M., Hausman R.E. The Cell: A Molecular Approach. Volume 2 Sinauer Associates; Sunderland, MA, USA: 2000.
-
- Mohandas N., Chasis J. Red blood cell deformability, membrane material properties and shape: Regulation by transmembrane, skeletal and cytosolic proteins and lipids. Semin. Hematol. 1993;30:171–192. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases

