A " Blood Relationship" Between the Overlooked Minimum Lactate Equivalent and Maximal Lactate Steady State in Trained Runners. Back to the Old Days?

Abstract

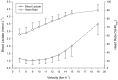
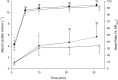
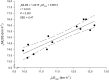
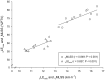
Maximal Lactate Steady State (MLSS) and Lactate Threshold (LT) are physiologically-related and fundamental concepts within the sports and exercise sciences. Literature supporting their relationship, however, is scarce. Among the recognized LTs, we were particularly interested in the disused "Minimum Lactate Equivalent" (LE_min), first described in the early 1980s. We hypothesized that velocity at LT, conceptually comprehended as in the old days (LE_min), could predict velocity at MLSS (_VMLSS) more accurate than some other blood lactate-related thresholds (BL_RTs) routinely used nowadays by many sport science practitioners. Thirteen male endurance-trained [_VMLSS 15.0 ± 1.1 km·h^-1; maximal oxygen uptake ( ${\stackrel{.}{V}O}_{2max}$ ) 67.6 ± 4.1 ml·kg^-1·min^-1] homogeneous (coefficient of variation: ≈7%) runners conducted 1) a submaximal discontinuous incremental running test to determine several BL_RTs followed by a maximal ramp incremental running test for ${\stackrel{.}{V}O}_{2max}$ determination, and 2) several (4-5) constant velocity running tests to determine _VMLSS with a precision of 0.20 km·h^-1. Determined BL_RTs include LE_min and LE_min-related LE_min plus 1 (LE_min+1mM) and 1.5 mmol·L^-1 (LE_min+1.5mM), along with well-established BL_RTs such as conventionally-calculated LT, D_max and fixed blood lactate concentration thresholds. LE_min did not differ from LT (P = 0.71; ES: 0.08) and was 27% lower than MLSS (P < 0.001; ES: 3.54). LE_min+1mM was not different from MLSS (P = 0.47; ES: 0.09). LE_min was the best predictor of _VMLSS (r = 0.91; P < 0.001; SEE = 0.47 km·h^-1), followed by LE_min+1mM (r = 0.86; P < 0.001; SEE = 0.58 km·h^-1) and LE_min+1.5mM (r = 0.84; P < 0.001; SEE = 0.86 km·h^-1). There was no statistical difference between MLSS and estimated MLSS using LE_min prediction formula (P = 0.99; ES: 0.001). Mean bias and limits of agreement were 0.00 ± 0.45 km·h^-1 and ±0.89 km·h^-1. Additionally, LE_min, LE_min+1mM and LE_min+1.5mM were the best predictors of ${\stackrel{.}{V}O}_{2max}$ (r = 0.72-0.79; P < 0.001). These results support LE_min, an objective submaximal overlooked and underused BL_RT, to be one of the best single MLSS predictors in endurance trained runners. Our study advocates factors controlling LE_min to be shared, at least partly, with those controlling MLSS.

Keywords: Owles' point; aerobic capacity; aerobic threshold; anaerobic threshold; endurance assessment; lactate threshold; oxygen endurance performance limit; submaximal exercise testing.

Figure 1

Illustration of blood lactate-related thresholds (BL_RTs) determination in a representative participant. Dashed lines: second-order polynomial curve fits. Dotted lines: the greatest perpendicular distance from the third-order polynomial BLC-velocity curve fit to the generated straight line by the two end data-points of this curve. Note that for clearness of figure presentation, D_max determination is illustrated together with the rest of BL_RTs on a second-order polynomial curve fit, although actually it was determined on third-order curvilinear fits as originally described (Cheng et al., 1992).

Figure 2

Mean (SD) blood lactate and heart rate responses to the submaximal discontinuous incremental running exercise test. All subjects terminated the 15 km·h⁻¹ exercise stage. Mean (SD) values at completion of the test of subjects achieving ≥16 km·h⁻¹ are indicated by dashed lines.

Figure 3

Mean (SD) blood lactate (triangles) and heart rate (circles) responses to the constant running velocities tests (CVRTs) at the maximal lactate steady state velocity (open symbols) and at 0.2 km·h⁻¹ faster velocity (filled symbols). * Significantly different from the rest of the time-points within the same CVRT (P < 0.0125). ^#Significantly higher in comparison with the corresponding time-points at the maximal lactate steady state velocity CVRT (P < 0.0125).

Figure 4

Linear relationship between the velocity at the Minimum Lactate Equivalent (_VLE_min) and the velocity at the Maximal Lactate Steady State (_VMLSS). Solid line: linear regression. Dashed lines: 95% confidence intervals.

Figure 5

Linear regressions between the velocities at the Minimum Lactate Equivalent (_VLE_min) and Maximal Lactate Steady State (_VMLSS) in absolute values (km·h⁻¹) with their respective velocities relative to peak treadmill velocity (PTV).

Figure 6

Linear regression between heart rate (HR) at the Lactate Minimum Equivalent (_HRLE_min) and HR at min 5 of the constant velocity running test (CVRT) performed at the velocity of the maximal lactate steady state (_VMLSS).