Forward and inverse problems in the mechanics of soft filaments
- PMID: 30110439
- PMCID: PMC6030325
- DOI: 10.1098/rsos.171628
Forward and inverse problems in the mechanics of soft filaments
Abstract
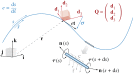
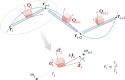
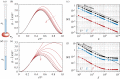
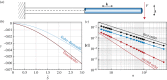
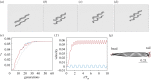
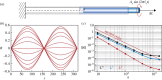
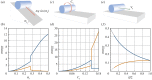
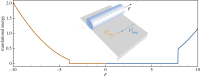
Soft slender structures are ubiquitous in natural and artificial systems, in active and passive settings and across scales, from polymers and flagella, to snakes and space tethers. In this paper, we demonstrate the use of a simple and practical numerical implementation based on the Cosserat rod model to simulate the dynamics of filaments that can bend, twist, stretch and shear while interacting with complex environments via muscular activity, surface contact, friction and hydrodynamics. We validate our simulations by solving a number of forward problems involving the mechanics of passive filaments and comparing them with known analytical results, and extend them to study instabilities in stretched and twisted filaments that form solenoidal and plectonemic structures. We then study active filaments such as snakes and other slender organisms by solving inverse problems to identify optimal gaits for limbless locomotion on solid surfaces and in bulk liquids.
Keywords: Cosserat theory; computational mechanics; soft filaments.
Conflict of interest statement
The authors declare no competing interests.
Figures








Similar articles
-
The asymptotic coarse-graining formulation of slender-rods, bio-filaments and flagella.J R Soc Interface. 2018 Jul;15(144):20180235. doi: 10.1098/rsif.2018.0235. J R Soc Interface. 2018. PMID: 29973402 Free PMC article.
-
Topology, Geometry, and Mechanics of Strongly Stretched and Twisted Filaments: Solenoids, Plectonemes, and Artificial Muscle Fibers.Phys Rev Lett. 2019 Nov 15;123(20):208003. doi: 10.1103/PhysRevLett.123.208003. Phys Rev Lett. 2019. PMID: 31809094
-
Friction modulation in limbless, three-dimensional gaits and heterogeneous terrains.Nat Commun. 2021 Oct 19;12(1):6076. doi: 10.1038/s41467-021-26276-x. Nat Commun. 2021. PMID: 34667170 Free PMC article.
-
Continuous body 3-D reconstruction of limbless animals.J Exp Biol. 2021 Mar 12;224(Pt 6):jeb220731. doi: 10.1242/jeb.220731. J Exp Biol. 2021. PMID: 33536306
-
Pepstatin A: polymerization of an oligopeptide.Micron. 1994;25(2):189-217. doi: 10.1016/0968-4328(94)90042-6. Micron. 1994. PMID: 8055247 Review.
Cited by
-
A Hybrid Controller for a Soft Pneumatic Manipulator Based on Model Predictive Control and Iterative Learning Control.Sensors (Basel). 2023 Jan 22;23(3):1272. doi: 10.3390/s23031272. Sensors (Basel). 2023. PMID: 36772312 Free PMC article.
-
Reversible kink instability drives ultrafast jumping in nematodes and soft robots.Sci Robot. 2025 Apr 23;10(101):eadq3121. doi: 10.1126/scirobotics.adq3121. Epub 2025 Apr 23. Sci Robot. 2025. PMID: 40267223 Free PMC article.
-
Modeling and simulation of complex dynamic musculoskeletal architectures.Nat Commun. 2019 Oct 23;10(1):4825. doi: 10.1038/s41467-019-12759-5. Nat Commun. 2019. PMID: 31645555 Free PMC article.
-
Reduced order modeling and model order reduction for continuum manipulators: an overview.Front Robot AI. 2023 Sep 15;10:1094114. doi: 10.3389/frobt.2023.1094114. eCollection 2023. Front Robot AI. 2023. PMID: 37779576 Free PMC article. Review.
-
Automated resolution of the spiral torsion spring inverse design problem.Sci Rep. 2024 Feb 5;14(1):2956. doi: 10.1038/s41598-024-53404-6. Sci Rep. 2024. PMID: 38316845 Free PMC article.
References
-
- Kirchhoff G. 1859. Ueber das gleichgewicht und die bewegung eines unendlich dünnen elastischen stabes. J. Reine Angew. Math. 56, 285–313. (doi:10.1515/crll.1859.56.285) - DOI
-
- Clebsch A. 1883. Théorie de l’élasticité des corps solides. Paris, France: Dunod.
-
- Love AEH. 1906. A treatise on the mathematical theory of elasticity. Cambridge, UK: Cambridge University Press.
-
- Cosserat E, Cosserat F. 1909. Théorie des corps déformables. Ithaca, NY: Cornell University Library.
-
- Antman SS. 1973. The theory of rods. Berlin, Germany: Springer.
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

