Forward and inverse problems in the mechanics of soft filaments
- PMID: 30110439
- PMCID: PMC6030325
- DOI: 10.1098/rsos.171628
Forward and inverse problems in the mechanics of soft filaments
Abstract
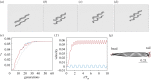
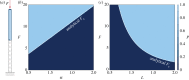
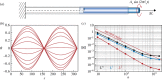
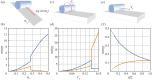
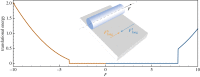
Soft slender structures are ubiquitous in natural and artificial systems, in active and passive settings and across scales, from polymers and flagella, to snakes and space tethers. In this paper, we demonstrate the use of a simple and practical numerical implementation based on the Cosserat rod model to simulate the dynamics of filaments that can bend, twist, stretch and shear while interacting with complex environments via muscular activity, surface contact, friction and hydrodynamics. We validate our simulations by solving a number of forward problems involving the mechanics of passive filaments and comparing them with known analytical results, and extend them to study instabilities in stretched and twisted filaments that form solenoidal and plectonemic structures. We then study active filaments such as snakes and other slender organisms by solving inverse problems to identify optimal gaits for limbless locomotion on solid surfaces and in bulk liquids.
Keywords: Cosserat theory; computational mechanics; soft filaments.
Conflict of interest statement
The authors declare no competing interests.
Figures
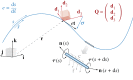
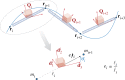

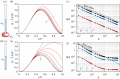
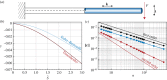
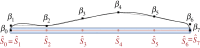

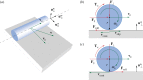
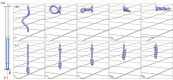
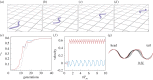





References
-
- Kirchhoff G. 1859. Ueber das gleichgewicht und die bewegung eines unendlich dünnen elastischen stabes. J. Reine Angew. Math. 56, 285–313. (doi:10.1515/crll.1859.56.285) - DOI
-
- Clebsch A. 1883. Théorie de l’élasticité des corps solides. Paris, France: Dunod.
-
- Love AEH. 1906. A treatise on the mathematical theory of elasticity. Cambridge, UK: Cambridge University Press.
-
- Cosserat E, Cosserat F. 1909. Théorie des corps déformables. Ithaca, NY: Cornell University Library.
-
- Antman SS. 1973. The theory of rods. Berlin, Germany: Springer.
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources
