Active nematics

Abstract

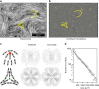
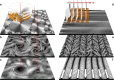
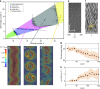
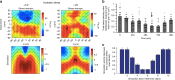
Active matter extracts energy from its surroundings at the single particle level and transforms it into mechanical work. Examples include cytoskeleton biopolymers and bacterial suspensions. Here, we review experimental, theoretical and numerical studies of active nematics - a type of active system that is characterised by self-driven units with elongated shape. We focus primarily on microtubule-kinesin mixtures and the hydrodynamic theories that describe their properties. An important theme is active turbulence and the associated motile topological defects. We discuss ways in which active turbulence may be controlled, a pre-requisite to harvesting energy from active materials, and we consider the appearance, and possible implications, of active nematics and topological defects to cellular systems and biological processes.

Fig. 1

Active nematic turbulence. a Fluorescence confocal microscopy micrograph of the active nematic in contact with an oil of 0.05 Pa s (see Supplementary Movie 1 where positive defects are tracked). b Snapshot of the time evolution from solving the continuum equations of motion, showing active turbulence. A comet-like, +1/2, and a trefoil-like, −1/2 defect are highlighted in each case. c Particle alignment and velocity fields around ±1/2 topological defects in extensile and contractile active systems. d Experimental distribution of vortex sizes in an active nematic in the regime of active turbulence, adapted from data in ref. , Nature Publishing Group. The solid line is an exponential fit to the data

Fig. 2

Alignment of an active nematic by anisotropic soft interfaces. In a–c the active nematic is in contact with an unconstrained smectic-A phase. In d–f, an external magnetic field (H) has aligned the smectic-A. In a and d the confocal reflection micrographs show the structure of the smectic-A phase at the interface with the aqueous phase in each case. The diagrams are sketches indicating the ordering of the smectic-A planes and liquid crystal molecules. b, e Fluorescence confocal micrographs of the active nematic layer with dynamical patterning that results from contact with the anisotropic interface. c, f Time averaged fluorescence confocal micrographs (total integration time 300 s). Arrows indicate the direction of the organised active flow. Field of view is 300 ×300 μm^,. (Adapted with permission from Nature Publishing Group and AIP Publishing)

Fig. 3

Flow states in active nematics confined to a 2D channel. a Regions of stability of different flow states as a function of the activity number, $A=L\sqrt{\zeta ∕K}$, which characterizes the ratio of the channel width L to the active length scale $\sqrt{K∕\zeta }$, and a dimensionless +1/2 defect self-motility V, obtained by solving the continuum equations of active nematics (adapted with permission from Royal Society of Chemistry). b–d Representation of the flow states. The flow is confined by lateral walls in the horizontal direction. The colourmap corresponds to the normalized magnitude of the velocity and the yellow lines illustrate the trajectories of +1/2 defects within the channel. e, f Experimental realisation of laminar shear flow in a confined monolayer of fibroblast cells: cell orientations by phase contrast (e) and the line integral convolution method (f). g, h Increasing the channel width leads to an active Fréedericksz transition from a no flow to a spontaneous flow state as predicted by continuum active gel theory. The comparison of the experimental measurements (black squares) with the analytical predictions (orange solid lines) shows excellent agreement both for the (g) central angle and (h) the velocity (v_y) of the flow at the mid region of the channel. (Adapted with permission from Nature Publishing Group)

Fig. 4

Active nematic defects in biological systems. a Growing colony of E. coli bacteria (Copyright (2014) by the American Physical Society). The motion of +1/2 defects towards the growing interface can lead to shape changes of the colony. b Epithelial tissue of Madine–Darby canine kidney (MDCK) cells. Scale bar is 10 μm (Nature Publishing Group). Strong correlations between the position of +1/2 defects and cell death and extrusion have been reported. c Monolayer of neural progenitor stem cells (Nature Publishing Group). Cells are depleted from −1/2 defects (blue, trefoil symbols) and accumulate at +1/2 ones (red, comet-like symbols). d Dense monolayer of mouse fibroblast cells (Nature Publishing Group) showing −1/2 and +1/2 topological defects marked by blue and orange circles, respectively

Fig. 5

Stress patterns and density of topological defects. a Comparison of the isotropic stress around +1/2 (left) and −1/2 (right) topological defects between the experiments on monolayers of MDCK cells and continuum numerical simulations of active nematics. Colourmaps show the magnitude of the isotropic stress with blue (red) corresponding to mechanical compression (tension). b, c Total defect areal density evolution as a function of time. In the experiments (b) blebbistatin was introduced at t = 0 to suppress the cell motility and was washed out at the time 600 min (shown by an arrow). Similarly in the simulation (c) the activity parameter decreased at simulation time t = 0, then increased at t = 5. (Nature Publishing Group)

Fig. 6

Active shells embedded in a nematic liquid crystal. a A spherical inclusion in a homogeneous nematic liquid crystal leads to the formation of an annular disclination (Saturn Ring). b, c Fluorescence micrographs showing the evolution of an active nematic spherical shell with four +1/2 defects (two visible at a given time), marked with yellow contours. d–f Brightfield micrographs with the oscillations of the Saturn Ring that has formed around an active shell. g–i Sketches showing the structure of the Saturn Ring in the micrographs (d–f). Scales are 20 μm. (Adapted with permission from American Association for the Advancement of Science)