Inferring hidden structure in multilayered neural circuits
- PMID: 30138312
- PMCID: PMC6124781
- DOI: 10.1371/journal.pcbi.1006291
Inferring hidden structure in multilayered neural circuits
Abstract
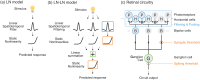
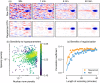
A central challenge in sensory neuroscience involves understanding how neural circuits shape computations across cascaded cell layers. Here we attempt to reconstruct the response properties of experimentally unobserved neurons in the interior of a multilayered neural circuit, using cascaded linear-nonlinear (LN-LN) models. We combine non-smooth regularization with proximal consensus algorithms to overcome difficulties in fitting such models that arise from the high dimensionality of their parameter space. We apply this framework to retinal ganglion cell processing, learning LN-LN models of retinal circuitry consisting of thousands of parameters, using 40 minutes of responses to white noise. Our models demonstrate a 53% improvement in predicting ganglion cell spikes over classical linear-nonlinear (LN) models. Internal nonlinear subunits of the model match properties of retinal bipolar cells in both receptive field structure and number. Subunits have consistently high thresholds, supressing all but a small fraction of inputs, leading to sparse activity patterns in which only one subunit drives ganglion cell spiking at any time. From the model's parameters, we predict that the removal of visual redundancies through stimulus decorrelation across space, a central tenet of efficient coding theory, originates primarily from bipolar cell synapses. Furthermore, the composite nonlinear computation performed by retinal circuitry corresponds to a boolean OR function applied to bipolar cell feature detectors. Our methods are statistically and computationally efficient, enabling us to rapidly learn hierarchical non-linear models as well as efficiently compute widely used descriptive statistics such as the spike triggered average (STA) and covariance (STC) for high dimensional stimuli. This general computational framework may aid in extracting principles of nonlinear hierarchical sensory processing across diverse modalities from limited data.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures








References
-
- Van Steveninck RDR, Bialek W. Real-time performance of a movement-sensitive neuron in the blowfly visual system: coding and information transfer in short spike sequences. Proceedings of the Royal Society of London B: Biological Sciences. 1988;234(1277):379–414. 10.1098/rspb.1988.0055 - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

