Dorsal anterior cingulate-brainstem ensemble as a reinforcement meta-learner

Abstract

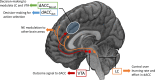
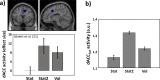
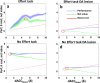
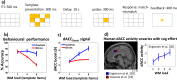
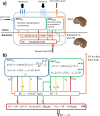
Optimal decision-making is based on integrating information from several dimensions of decisional space (e.g., reward expectation, cost estimation, effort exertion). Despite considerable empirical and theoretical efforts, the computational and neural bases of such multidimensional integration have remained largely elusive. Here we propose that the current theoretical stalemate may be broken by considering the computational properties of a cortical-subcortical circuit involving the dorsal anterior cingulate cortex (dACC) and the brainstem neuromodulatory nuclei: ventral tegmental area (VTA) and locus coeruleus (LC). From this perspective, the dACC optimizes decisions about stimuli and actions, and using the same computational machinery, it also modulates cortical functions (meta-learning), via neuromodulatory control (VTA and LC). We implemented this theory in a novel neuro-computational model-the Reinforcement Meta Learner (RML). We outline how the RML captures critical empirical findings from an unprecedented range of theoretical domains, and parsimoniously integrates various previous proposals on dACC functioning.

Fig 1. RML overview with neuroanatomical mapping.

The RML consists of a state-action selection dual system (dACC_Act and dACC_Boost), based on RL algorithms, and a parameter modulation system via catecholamine release (VTA and LC) that are in constant interaction. Finally, the RML can be connected to an external neural model (e.g. a fronto-parietal network) and part of the LC output (NE) can be used to modulate its activity while the entire system (RML + external model) is interacting with the environment.

Fig 2. Simulation 1: Methods and results.

a) The task (2-armed bandit) is represented like a binary choice task (blue or red squares), where the model decisions are represented as joystick movements. After each choice, the model received either a reward (sun) or not (cross). b) Example of task design with time line of statistical environments (order of presentation of different environments was randomized across simulations). The plot shows reward probability linked to each option (blue or red) as a function of trial number. In this case the model executed the task first in a stationary environment (Stat), then in a stationary environment with high uncertainty (Stat2), and finally in a volatile (Vol) environment. c) Learning rate (λ) time course (average across simulations ± s.e.m.). As the order of statistical environments was randomized across simulations, each simulation time course was sorted as Stat-Stat2-Vol. d, e) Average ∠ (across time and simulations) as a function of environmental volatility (± s.e.m.) in the RML (d) and humans (e; modified from: [30]). f) human pupil size (proxy of LC activity [–36]) during the same task.

Fig 3. Simulation 1: Results comparison with fMRI data.

a) Outcome-locked activation of human dACC (with 90% CI, extracted from the ROI indicated by the blue sphere; MNI: [12,14,44]) in a RL task executed during fMRI scanning. Data extracted by WebPlotDigitizer from Fig 4 in ref. [21]. The ROI is a local maximum within the cluster with the highest z value. The task was performed in the same three environments we used in our simulations. dACC activity peaked in Stat2 and not in Vol condition (Stat2 > Vol, p < 0.05), indicating responsiveness to overall uncertainty (i.e. PE) rather than to volatility (see ref. [21] for further details) b) dACC_Act average activity (sum of PE units activity ± s.e.m.; see Eq 1 and Equations S3-S4 in S1 File) as a function of environmental uncertainty. Differently from the LC, the dACC_Act is maximally active in stationary uncertain environments (Stat2), indicating that due to PE computation, dACC_Act (like the human dACC) codes for overall uncertainty rather than for volatility.

Fig 4. Simulation 2a: Methods and Results.

a) Effort task, where a high effort choice (thick arrow from joystick) leading to high reward (HR, large sun) was in competition with a low effort choice (thin arrow) leading to low reward (LR, small sun). b) Behavioural results (average HR/(LR+HR) ratio ±s.e.m., and average Stay/(LR+HR+Stay) choices ratio percentage ±s.e.m.) from RML and c) empirical data from rodents [47], in controls (blue), DA lesioned (red) and ACC lesioned (green) subjects. d) No Effort task, same as a) but with both options implying a low effort (thin black arrows). e) dACC_Boost efferent signal (boosting level b) time course over trials (average across simulations ± s.e.m.). f) dACC_Boost efferent signal (b; average across time and simulations) as a function of task type (Effort or No Effort task) and DA lesion. The boosting value is higher in the Effort task (main effect of task), but there is also a task x lesion interaction indicating the dACC_Boost attempts to compensate the loss of DA in the No Effort task (see main text). Results from the dACC lesion are not reported, as the simulated lesion targeted the dACC itself, leading to an obvious reduction of dACC_Boost activity. g) LC activity as a function of physical effort in the rhesus monkey [35]. Like in the RML (panel f, blue plot), the LC activity (controlled by the dACC_Boost) is higher for high effort condition. h) RML net subjective value computed in both dACC modules (sum of net values from both dACC modules, Equation S18 in S1 File) for the HR choice as a function of effort. i) Like in the human brain [44] the RML dACC computes also the net value (i.e. the value discounted by the expected cost) of choices.

Fig 5. Cost-benefits plots and optimal control of b in the dACC_Boost module.

To obtain these plots we systematically clamped b at several values (from 1 to 10, x axis of each plot) and then we administered the same paradigms of Fig 4B and 4D (all the combinations Effort x DA lesion). In all the plots, y axis represents simultaneously performance in terms of average reward signal to dACC_Boost (blue plots), boosting cost (red plots) and net value (performance–boost cost, described by Eq 6B). a) Effort task, no lesion. Plot showing RML behavioural performance as a function of b (blue plot), boosting cost (red plot, Eq 6B in Methods) and net value for the dACC_Boost module (green plot, resulting from Eq 6B). Red dotted circles highlight the optimal b value which maximizes the final net reward signal received by the dACC_Boost module. (maximum of green plot) b) Effort task, DA lesion. Same as a), but in this case the RML was DA lesioned. Due to lower average reward signal (blue plot), the net value (green) decreases monotonically, because the cost of boosting (red plot) did not change. Red dotted circle highlights the optimal b value, which is lower than in a). It must be considered that, although the optimal b value is 1, the average b (as shown in figures 5b and s11b) is biased toward higher values, as it is selected by a stochastic process (Eq 4) and values lower than 1 are not possible (asymmetric distribution). c) No Effort task, no lesion. In this case, being the task easy, the RML reaches a maximal performance without high values of b (blue plot is flat), therefore the optimal b value is low also in this case. d) No Effort task, DA lesion. As shown also in Fig 4B, in this case the optimal b value (dotted circle), is higher than in c), because a certain amount of boosting is necessary to avoid the preference for “Stay” option, which has no costs but also provides no reward. This ensures a minimal behavioural energization to prevent apathy and get a large reward paying a minimal cost (as it is a No Effort task). Plots are average on 40 simulations, error shadows mean s.e.m.

Fig 6. Recovery of HR option preference after DA lesion.

a) Double Effort task, where both options implied high effort. b) Recovery of the preference for HR option (HR/(HR+LR)) when a No Effort task is administered after an Effort task session (Effort → No Effort, blue plot), in both RML and c) animals [47] (mean percentage ± s.e.m.). Same phenomenon when a Double Effort session follows an Effort one (Effort → Double Effort, red plot). Note that in this case the number of “Stay” choices (Stay/number of trials) increased, simulating the emergence of apathic behaviour.

Fig 7. Simulation 2c: Methods and results.

a) Delayed Matching-to-sample task: events occurring in one trial. b) RML behavioural performance as a function of memory load and DA lesion (±s.e.m.). c) dACC_Boost output as a function of memory load and DA lesion (±s.e.m). d) Local maxima in which human dACC activity covaries with cognitive effort (left) and dACC activity as a function of memory load in a WM task ref (right, from blue coordinates).

Fig 8. Simulation 3a-b: Methods and results.

a) Experimental paradigm for higher-order classical conditioning (lower row) and cue-locked VTA response (upper row). The task consisted of a sequence of conditioned stimuli (colored disks) followed by primary reward (sun). Already at the second conditioning order, VTA activity results almost absent. b) During a higher-order instrumental conditioning (lower row), the VTA response (upper row) remains sustained up to the third order. c) Average dACC_Boost efferent signal (b± s.e.m.) in classical and instrumental paradigms. In instrumental paradigm the efferent boosting signal is higher, enhancing the VTA activity over different conditioning orders.

Fig 9. RML overview with equations.

a) The RML-environment interaction happens through nine channels of information exchange (black arrows) (input = empty bars; output = filled bars). The input channels consist of one channel encoding action costs (C), three channels encoding environmental states (s), and one channel encoding primary rewards (RW). The output consists of three channels coding each for one specific action (a), plus one channel conveying LC signals to other brain areas (NE). The entire model is composed of four reciprocally connected modules (each in a different color). The upper modules (blue and green) simulate the dACC, while the lower modules (red and orange) simulate the brainstem catecholamine nuclei (VTA and LC). dACC_Act selects actions directed toward the environment and learns through first and higher-order conditioning, while dACC_Boost modulates catecholamine nuclei output. The VTA module provides DA training signals to both dACC modules. The LC controls learning rate (λ; yellow bidirectional arrow) in both dACC modules, and effort exertion (promoting effortful actions) in the dACC_Act module (orange arrow), influencing their decisions. Finally, the LC signal controlling effort in the dACC_Act can be directed also toward other cognitive modules for neuro-modulation. b) Model overview with equations embedded. The equations are reported in their discrete form. Communication between modules is represented by arrows, with corresponding variables near each arrow. Variables δ and δ_B represent the prediction errors from respectively Eqs 1 and 3.