Analytic modeling of conductively anisotropic neural tissue

Abstract

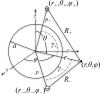
The abdominal ganglion of the Aplysia californica is an established in vitro model for studying neuroelectric behavior in the presence of an applied electrical current and recently used in studies of magnetic resonance electrical impedance tomography (MREIT) which allows for quantitative visualization of spatially distributed current and magnetic flux densities. Understanding the impact the Aplysia geometry and anisotropic conductivity have on applied electromagnetic fields is central to intepreting and refining MREIT data and protocols, respectively. Here we present a simplified bidomain model of an in vitro experimental preparation of the Aplysia abdominal ganglion, describing the tissue as a radially anisotropic sphere with equal anisotropy ratios, i.e., where radial conductivities in both intra- and extra-cellular regions are ten times that of their polar and azimuthal conductivities. The fully three dimensional problem is validated through comparisons with limiting examples of 2D isotropic analyses. Results may be useful in validating finite element models of MREIT experiments and have broader relevance to analysis of MREIT data obtained from complex neural architecture in the human brain.

FIG. 1.

Sphere with radius r = a in an infinite conducting medium with current source ⊕ and sink $\ominus$ points at ${\overrightarrow{p}}_{+}=(r_{+},{\theta }_{+},{\phi }_{+})$ and ${\overrightarrow{p}}_{-}=(r_{-},{\theta }_{-},{\phi }_{-})$, respectively. The dotted-dashed curves labeled as γ are the angles between the points' position vectors and that of a field point $\overrightarrow{r}=(r,\theta ,\phi )$.

FIG. 2.

The top, middle, and bottom rows are plots of the electric potential, current density, and magnetic flux density, respectively, in the plane z = 0. The dashed white line indicates the circumference of the sphere. In the Cartesian coordinates on this graph, the current point source is at (0, −5) and the current point sink is at (−5, 0). In the columns, from left to right, the ratio of ${\sigma }_o^l$ to σ_e is 1, 10, and 0.1, respectively. In the top graph, we show the extracellular potential of the sphere of tissue amid the external potential in the conducting bath. There the black lines are equipotentials, and the shade of color corresponds to the magnitude. In the middle graph, we show the external current density in the bath and the sum of the intracellular and extracellular current densities in the sphere. The magnetic flux density shown in the bottom graph was calculated from the current density field.

FIG. 3.

(a) A contour plot of the extracellular potential of the sphere of tissue amid the external potential in the conducting bath. The dashed gray line indicates the circumference of the sphere. The black lines are equipotentials, and the shade of color corresponds to the magnitude. In the Cartesian coordinates on this graph, the current point source is at (5, 0) and the current point sink is at (−5, 0). The ratio ρ_e/ρ_o = 1. (b) The intracellular (dotted-dashed), extracellular (solid), transmembrane (dotted), and bath (dashed) potentials are shown as a function of x, along the white line where y = 0 in (a). The vertical lines at x = −2 and 2 correspond to the radius of the sphere, r = a, where are also plotted the lines tangent to the curves of the potentials in the boundary conditions.