High-dimensional entanglement between distant atomic-ensemble memories
- PMID: 30167124
- PMCID: PMC6059826
- DOI: 10.1038/lsa.2016.157
High-dimensional entanglement between distant atomic-ensemble memories
Abstract
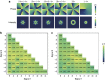
Entangled quantum states in high-dimensional space show many advantages compared with entangled states in two-dimensional space. The former enable quantum communication with higher channel capacity, enable more efficient quantum-information processing and are more feasible for closing the detection loophole in Bell test experiments. Establishing high-dimensional entangled memories is essential for long-distance communication, but its experimental realization is lacking. We experimentally established high-dimensional entanglement in orbital angular momentum space between two atomic ensembles separated by 1 m. We reconstructed the density matrix for a three-dimensional entanglement and obtained an entanglement fidelity of (83.9±2.9)%. More importantly, we confirmed the successful preparation of a state entangled in more than three-dimensional space (up to seven-dimensional) using entanglement witnesses. Achieving high-dimensional entanglement represents a significant step toward a high-capacity quantum network.
Keywords: high-dimensional entanglement; orbital angular momentum; quantum memory.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
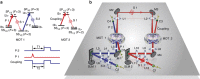
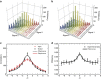
 , with (y0=0, xc=0, w=7.7, A=2030) and (y0=12.7, xc=0, w=4.57, A=1463), respectively. (d) The efficiency of storing different OAM modes. The black curve is calculated using the same fitting function, with fitted values (y0=0.132, xc=0, w=2.274, A=0.354); w specifies the half-width at half-maximum of y. We identify w with the effective quantum spiral bandwidth. For panels c and d, the correlation refers to the coincidences of signal 1 and 2 photons, while the efficiency corresponds to the ratio of the coincidences before and after storage. Error bars represent ±s.d.
, with (y0=0, xc=0, w=7.7, A=2030) and (y0=12.7, xc=0, w=4.57, A=1463), respectively. (d) The efficiency of storing different OAM modes. The black curve is calculated using the same fitting function, with fitted values (y0=0.132, xc=0, w=2.274, A=0.354); w specifies the half-width at half-maximum of y. We identify w with the effective quantum spiral bandwidth. For panels c and d, the correlation refers to the coincidences of signal 1 and 2 photons, while the efficiency corresponds to the ratio of the coincidences before and after storage. Error bars represent ±s.d.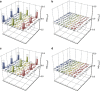
Similar articles
-
Twisted photons: new quantum perspectives in high dimensions.Light Sci Appl. 2018 Mar 9;7:17146. doi: 10.1038/lsa.2017.146. eCollection 2018. Light Sci Appl. 2018. PMID: 30839541 Free PMC article. Review.
-
Experimental realization of entanglement in multiple degrees of freedom between two quantum memories.Nat Commun. 2016 Nov 14;7:13514. doi: 10.1038/ncomms13514. Nat Commun. 2016. PMID: 27841274 Free PMC article.
-
Quantum storage of orbital angular momentum entanglement in an atomic ensemble.Phys Rev Lett. 2015 Feb 6;114(5):050502. doi: 10.1103/PhysRevLett.114.050502. Epub 2015 Feb 4. Phys Rev Lett. 2015. PMID: 25699427
-
Entanglement distillation for quantum communication network with atomic-ensemble memories.Opt Express. 2014 Oct 6;22(20):23897-911. doi: 10.1364/OE.22.023897. Opt Express. 2014. PMID: 25321967
-
Quantum entanglement in photoactive prebiotic systems.Syst Synth Biol. 2014 Jun;8(2):117-40. doi: 10.1007/s11693-014-9138-6. Epub 2014 Mar 25. Syst Synth Biol. 2014. PMID: 24799958 Free PMC article. Review.
Cited by
-
Twisted photons: new quantum perspectives in high dimensions.Light Sci Appl. 2018 Mar 9;7:17146. doi: 10.1038/lsa.2017.146. eCollection 2018. Light Sci Appl. 2018. PMID: 30839541 Free PMC article. Review.
-
Deterministic secure quantum communication using a single d-level system.Sci Rep. 2017 Mar 22;7:44934. doi: 10.1038/srep44934. Sci Rep. 2017. PMID: 28327557 Free PMC article.
-
Experimental realization of a multiplexed quantum memory with 225 individually accessible memory cells.Nat Commun. 2017 May 8;8:15359. doi: 10.1038/ncomms15359. Nat Commun. 2017. PMID: 28480891 Free PMC article.
-
Multidimensional entanglement transport through single-mode fiber.Sci Adv. 2020 Jan 24;6(4):eaay0837. doi: 10.1126/sciadv.aay0837. eCollection 2020 Jan. Sci Adv. 2020. PMID: 32042899 Free PMC article.
-
Orbital angular momentum of photons and the entanglement of Laguerre-Gaussian modes.Philos Trans A Math Phys Eng Sci. 2017 Feb 28;375(2087):20150442. doi: 10.1098/rsta.2015.0442. Philos Trans A Math Phys Eng Sci. 2017. PMID: 28069773 Free PMC article. Review.
References
-
- Kimble HJ. The quantum internet. Nature 2008; 453: 1023–1030. - PubMed
-
- Briegel HJ, Dür W, Cirac JI, Zoller P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys Rev Lett 1998; 81: 5932.
-
- Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature 2001; 412: 313–316. - PubMed
-
- Franke-Arnold S, Allen L, Padgett M. Advances in optical angular momentum. Laser Photon Rev 2008; 2: 299–313.
-
- Yao AM, Padgett MJ. Orbital angular momentum: origins, behavior and applications. Adv Opt Photon 2011; 3: 161–204.
LinkOut - more resources
Full Text Sources
Other Literature Sources

