Experimental quantum secure direct communication with single photons

Abstract

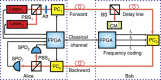
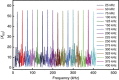
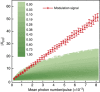
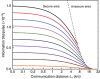
Quantum secure direct communication is an important mode of quantum communication in which secret messages are securely communicated directly over a quantum channel. Quantum secure direct communication is also a basic cryptographic primitive for constructing other quantum communication tasks, such as quantum authentication and quantum dialog. Here, we report the first experimental demonstration of quantum secure direct communication based on the DL04 protocol and equipped with single-photon frequency coding that explicitly demonstrated block transmission. In our experiment, we provided 16 different frequency channels, equivalent to a nibble of four-bit binary numbers for direct information transmission. The experiment firmly demonstrated the feasibility of quantum secure direct communication in the presence of noise and loss.

Keywords: DL04 protocol; block transmission; channel loss and noise; quantum secure direct communication; single-photon frequency coding.

Figure 1

Schematic diagram of the experimental setup of the FRECO-DL04 protocol. PBS, Polarization beam splitter; Att, Variable attenuator; PC, Polarization controller; BS, Beam splitter; CM, Control mode; FPGA, Field programmable gate array; SPD, Single-photon detector. The distance between Alice and Bob is L₁, and the delay line length is L₂.

Figure 2

The experimental results of the modulation frequency spectrum. The y-axis is the Fourier-transformed amplitude in Equation (3). The different color lines represent different modulation frequencies. These 16 modulation frequency spectrum lines correspond to binary numbers from 0000 to 1111. The systematic pulse repetition frequency is 10 MHz.

Figure 3

The characteristic spectrum and background noise distribution of the modulation frequency spectrum. The x-axis is the mean photon count per pulse that Alice detects. The green colored areas are the background white noise in the experiment, where the color depth represents the relative probability distribution of the noise. The red line represents the amplitude of the characteristic spectrum. The modulation frequency is 200 kHz.

Figure 4

The calculated transmitted information bit per pulse versus the communication distance. The dotted line is the cut-off line of the secure communication area. The solid lines with different colors represent different mean photon numbers per pulse (μ=0.19, 0.17, 0.15, 0.13, 0.11, 0.09, 0.07, 0.05, 0.03, 0.01, from top to bottom). Here, η_det=0.32, e=5‰, α=0.2 dB km⁻¹, L₂=L₁, and C=1/2.