Particle manipulation beyond the diffraction limit using structured super-oscillating light beams
- PMID: 30167295
- PMCID: PMC6062334
- DOI: 10.1038/lsa.2017.50
Particle manipulation beyond the diffraction limit using structured super-oscillating light beams
Abstract
The diffraction-limited resolution of light focused by a lens was derived in 1873 by Ernst Abbe. Later in 1952, a method to reach sub-diffraction light spots was proposed by modulating the wavefront of the focused beam. In a related development, super-oscillating functions, that is, band-limited functions that locally oscillate faster than their highest Fourier component, were introduced and experimentally applied for super-resolution microscopy. Up till now, only simple Gaussian-like sub-diffraction spots were used. Here we show that the amplitude and phase profile of these sub-diffraction spots can be arbitrarily controlled. In particular, we utilize Hermite-Gauss, Laguerre-Gauss and Airy functions to structure super-oscillating beams with sub-diffraction lobes. These structured beams are then used for high-resolution trapping and manipulation of nanometer-sized particles. The trapping potential provides unprecedented localization accuracy and stiffness, significantly exceeding those provided by standard diffraction-limited beams.
Keywords: beam shaping; optical tweezers; optical vortex; super-oscillating beams.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


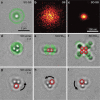
 from the SO-vortex beam to the trapped beads.
from the SO-vortex beam to the trapped beads.
References
-
- Dholakia K, Čižmár T. Shaping the future of manipulation. Nat Photon 2011; 5: 335–342.
-
- Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A 1992; 45: 8185–8190. - PubMed
-
- He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys Rev Lett 1995; 75: 826–829. - PubMed
-
- Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of accelerating airy beams. Phys Rev Lett 2007; 99: 213901. - PubMed
-
- Zhang P, Hu Y, Li TC, Cannan D, Yin XB et al. Nonparaxial Mathieu and weber accelerating beams. Phys Rev Lett 2012; 109: 193901. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

