Generalized Score Functions for Causal Discovery

Abstract

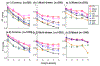
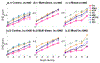
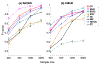
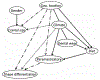
Discovery of causal relationships from observational data is a fundamental problem. Roughly speaking, there are two types of methods for causal discovery, constraint-based ones and score-based ones. Score-based methods avoid the multiple testing problem and enjoy certain advantages compared to constraint-based ones. However, most of them need strong assumptions on the functional forms of causal mechanisms, as well as on data distributions, which limit their applicability. In practice the precise information of the underlying model class is usually unknown. If the above assumptions are violated, both spurious and missing edges may result. In this paper, we introduce generalized score functions for causal discovery based on the characterization of general (conditional) independence relationships between random variables, without assuming particular model classes. In particular, we exploit regression in RKHS to capture the dependence in a non-parametric way. The resulting causal discovery approach produces asymptotically correct results in rather general cases, which may have nonlinear causal mechanisms, a wide class of data distributions, mixed continuous and discrete data, and multidimensional variables. Experimental results on both synthetic and real-world data demonstrate the efficacy of our proposed approach.

Figure 1:

(a) Scatter plot of the estimated noise Ê₁ and Ê₃; Ê₁ and Ê₃ are correlated. (b) Scatter plot of X₁ and X₂; they are uncorrelated.

Figure 2:

The F1 score of recovered causal graphs. (a.1) Continuous data with n = 500. (a.2) Continuous data with n = 1000. (b.1) Multi-dimensional data with n = 500. (b.2) Multi-dimensional data with n = 1000. (c.1) Mixed continuous and discrete data with n = 500. (c.2) Mixed continuous and discrete data with n = 1000. The x-axis is the graph density. The y-axis is the F1 score; higher F1 score means higher accuracy.

Figure 3:

The normalized SHD of recovered causal graphs. The y-axis is the normalized SHD score; the lower SHD score means better accuracy.

Figure 4:

The F1 score of the recovered causal graphs on the two discrete networks. (a) CHILD network. (b) SACHS network.

Figure 5:

Recovered causal graph from Archaeology data set. The solid lines are shared edges from the CV likelihood and the marginal likelihood. The dashed edges are recovered only by CV likelihood, and the dotted edges are recovered only by marginal likelihood.