Caenorhabditis elegans and the network control framework-FAQs

Abstract

Control is essential to the functioning of any neural system. Indeed, under healthy conditions the brain must be able to continuously maintain a tight functional control between the system's inputs and outputs. One may therefore hypothesize that the brain's wiring is predetermined by the need to maintain control across multiple scales, maintaining the stability of key internal variables, and producing behaviour in response to environmental cues. Recent advances in network control have offered a powerful mathematical framework to explore the structure-function relationship in complex biological, social and technological networks, and are beginning to yield important and precise insights on neuronal systems. The network control paradigm promises a predictive, quantitative framework to unite the distinct datasets necessary to fully describe a nervous system, and provide mechanistic explanations for the observed structure and function relationships. Here, we provide a thorough review of the network control framework as applied to Caenorhabditis elegans (Yan et al. 2017 Nature550, 519-523. (doi:10.1038/nature24056)), in the style of Frequently Asked Questions. We present the theoretical, computational and experimental aspects of network control, and discuss its current capabilities and limitations, together with the next likely advances and improvements. We further present the Python code to enable exploration of control principles in a manner specific to this prototypical organism.This article is part of a discussion meeting issue 'Connectome to behaviour: modelling C. elegans at cellular resolution'.

Keywords: C. elegans; connectome; control theory; locomotion; network science.

Figure 1.

The network control approach to understanding the behavioural responses of C. elegans. Graphical representation of the proposed control framework (adapted from [12]). According to structural controllability in the context of a locomotory response to stimuli, if removal of a neuron disrupts controllability of the muscles, we designate it ‘Essential’ for locomotion; if not, we call it ‘Non-essential’. To make this assessment, we first mapped the C. elegans responsive locomotor behaviours into a target network control problem, asking to what degree the sensory neurons (blue) can control the muscles (pink). This allowed us to predict the previously unknown involvement of neuron PDB in C. 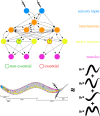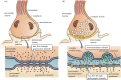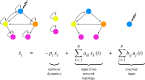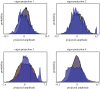elegans locomotion, and functional differences between individual neurons within the DD neuronal class. We test our predictions through cell-specific laser ablation and worm-tracking experiments, and statistically comparing eigenworm features. The original electron microscopy (EM) images in White et al. [16] were reconstructed from five partial worms—primarily N2U and JSE (adult hermaphrodites), then N2T for the anterior nerve ring (adult hermaphrodite), N2Y (adult male) for the section between N2U and JSE, and finally JSH (L4 larva) to check connectivity in the nerve ring (adapted from [17] and [12]). C. elegans moves in a sinusoidal fashion, via dorsoventral bends. Its 95 rhomboid body wall muscle cells are arranged as staggered paired rows in four quadrants (dorsal left/right and ventral left/right), and each muscle cell receives multiple inputs from some of the 75 motor neurons. Corresponding muscles contract and relax in a reciprocal fashion (e.g. for a dorsal bend, the dorsal muscle cells contract while their ventral counterparts relax), and movement requires these waveforms to be propagated sequentially to neighbouring muscle cells, along the length of the animal, in the correct direction. For movement to be sustained, oscillation between the contracted and relaxed states is required. The structure of the motor circuit is critical to achieving these basic requirements. The motor neurons themselves receive input from the ‘command’ interneurons, which constitute a bistable circuit that determines the direction of movement, depending on input from sensory neurons (reviewed by [–20]). The posture of the worm can be reconstructed as a summation of eigenworms, and we consider the leading four eigen projections, (shown on the bottom right as a₁x to a₄x), which account for 95% of the variance in body shape, as a basis set [21,22].

Figure 2.

Chemical synapses and electrical gap junctions. Chemical synapses and electrical gap junctions have very different properties and underlying mechanisms. In electrical gap junctions (a), voltage is transferred via touching membranes and signals may pass in both directions. In chemical synapses (b), signals are transferred through ion channels from the pre- to postsynaptic neuron.

Figure 3.

Intrinsic dynamics and self-loops. The dynamics of many real networks—including neuronal networks—may be modelled as a simple set of ordinary differential equations [51,52], with terms to account for (i) the intrinsic dynamics of the nodes; (ii) the input signals from other nodes in the network resulting from network topology; and (iii) any external input signals. The intrinsic dynamics manifest as self-loops. We can assume that neurons have one type of self-loop, and muscles have another [12].

Figure 4.

Eigenworm feature statistics for the voltage-gated calcium channel mutant unc-2(gk366). This allele is a deletion of the voltage-gated calcium channel gene unc-2, and mutant animals are hence strongly defective in neurotransmission from all neurons. The four panels depict the probability distributions of the first four eigen projections, for wild-type (grey) and for the mutant unc-2(gk366) (blue). The y-axis shows the probability density (ΣP(x) = 1) and the x-axis shows the projected amplitude for each eigenworm (arbitrary units). While the distributions for the two strains are clearly different, there is significant overlap in the observed eigen projections. Reproduced with permission from the database described previously [56].

Figure 5.

Robustness of the predictions to imperfect data. Robustness analyses, testing the robustness of ablation predictions to up to 420 random weak link deletions (approximately 14% of the network).