Functional connectomics from neural dynamics: probabilistic graphical models for neuronal network of Caenorhabditis elegans
- PMID: 30201841
- PMCID: PMC6158227
- DOI: 10.1098/rstb.2017.0377
Functional connectomics from neural dynamics: probabilistic graphical models for neuronal network of Caenorhabditis elegans
Abstract
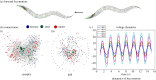
We propose an approach to represent neuronal network dynamics as a probabilistic graphical model (PGM). To construct the PGM, we collect time series of neuronal responses produced by the neuronal network and use singular value decomposition to obtain a low-dimensional projection of the time-series data. We then extract dominant patterns from the projections to get pairwise dependency information and create a graphical model for the full network. The outcome model is a functional connectome that captures how stimuli propagate through the network and thus represents causal dependencies between neurons and stimuli. We apply our methodology to a model of the Caenorhabditis elegans somatic nervous system to validate and show an example of our approach. The structure and dynamics of the C. elegans nervous system are well studied and a model that generates neuronal responses is available. The resulting PGM enables us to obtain and verify underlying neuronal pathways for known behavioural scenarios and detect possible pathways for novel scenarios.This article is part of a discussion meeting issue 'Connectome to behaviour: modelling C. elegans at cellular resolution'.
Keywords: Caenorhabditis elegans; functional connectome; neuronal networks; probabilistic graphical models.
© 2018 The Author(s).
Conflict of interest statement
We declare we have no competing interests.
Figures


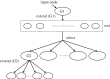



 sensory, motor
sensory, motor  motor, sensory
motor, sensory motor are zoomed in to compare detailed differences in gap, synaptic and PGM connections. Input neurons that activate the majority of the responding neurons are labelled.
motor are zoomed in to compare detailed differences in gap, synaptic and PGM connections. Input neurons that activate the majority of the responding neurons are labelled.


Similar articles
-
Connectome to behaviour: modelling Caenorhabditis elegans at cellular resolution.Philos Trans R Soc Lond B Biol Sci. 2018 Sep 10;373(1758):20170366. doi: 10.1098/rstb.2017.0366. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 30201832 Free PMC article.
-
c302: a multiscale framework for modelling the nervous system of Caenorhabditis elegans.Philos Trans R Soc Lond B Biol Sci. 2018 Sep 10;373(1758):20170379. doi: 10.1098/rstb.2017.0379. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 30201842 Free PMC article.
-
Low-dimensional functionality of complex network dynamics: neurosensory integration in the Caenorhabditis Elegans connectome.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 May;89(5):052805. doi: 10.1103/PhysRevE.89.052805. Epub 2014 May 12. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25353842
-
C. elegans wired and wireless connectome: insights into principles of nervous system structure and function.J Biosci. 2025;50:16. J Biosci. 2025. PMID: 40135746 Review.
-
Caenorhabditis elegans and the network control framework-FAQs.Philos Trans R Soc Lond B Biol Sci. 2018 Sep 10;373(1758):20170372. doi: 10.1098/rstb.2017.0372. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 30201837 Free PMC article. Review.
Cited by
-
Statistical perspective on functional and causal neural connectomics: The Time-Aware PC algorithm.PLoS Comput Biol. 2022 Nov 14;18(11):e1010653. doi: 10.1371/journal.pcbi.1010653. eCollection 2022 Nov. PLoS Comput Biol. 2022. PMID: 36374908 Free PMC article.
-
Novel Technological Advances in Functional Connectomics in C. elegans.J Dev Biol. 2019 Apr 23;7(2):8. doi: 10.3390/jdb7020008. J Dev Biol. 2019. PMID: 31018525 Free PMC article. Review.
-
Alternating chimera states and synchronization in multilayer neuronal networks with ephaptic intralayer coupling.Cogn Neurodyn. 2024 Dec;18(6):3847-3858. doi: 10.1007/s11571-024-10169-y. Epub 2024 Aug 31. Cogn Neurodyn. 2024. PMID: 39712137
-
The transcription factor unc-130/FOXD3/4 contributes to the biphasic calcium response required to optimize avoidance behavior.Sci Rep. 2022 Feb 3;12(1):1907. doi: 10.1038/s41598-022-05942-0. Sci Rep. 2022. PMID: 35115609 Free PMC article.
-
Multi-Omics and Genome-Scale Modeling Reveal a Metabolic Shift During C. elegans Aging.Front Mol Biosci. 2019 Feb 6;6:2. doi: 10.3389/fmolb.2019.00002. eCollection 2019. Front Mol Biosci. 2019. PMID: 30788345 Free PMC article.
References
-
- Koller D, Friedman N, Getoor L, Taskar B. 2007. Graphical models in a nutshell. In Introduction to statistical relational learning, pp. 13–55. Cambridge, MA: MIT press.
-
- Koller D, Friedman N. 2009. Probabilistic graphical models: principles and techniques. Cambridge, MA: MIT Press.
-
- Murphy KP. 2012. Machine learning: a probabilistic perspective. Cambridge, MA: MIT Press.
-
- Kolar M, Song L, Ahmed A, Xing EP. 2010. Estimating time-varying networks. Ann. Appl. Stat. 4, 94–123. (10.1214/09-aoas308) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

