Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Sep 10;18(9):3024.
doi: 10.3390/s18093024.

Fractional-Order PID Control Strategy on Hydraulic-Loading System of Typical Electromechanical Platform

Ning Wang  1 , Jianmei Wang  2 , Zhixiong Li  3   4 , Xuefeng Tang  5 , Dingbang Hou  6
Affiliations

Fractional-Order PID Control Strategy on Hydraulic-Loading System of Typical Electromechanical Platform

Ning Wang et al. Sensors (Basel). .

Abstract

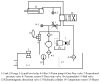
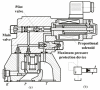
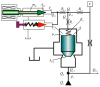
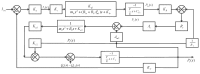
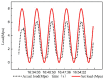
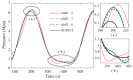
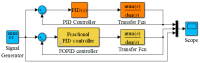
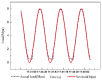
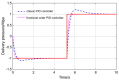
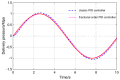
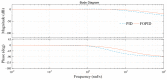
In this paper, a control method for a hydraulic loading system of an electromechanical platform based on a fractional-order PID (Proportion-Integration-Differentiation) controller is proposed, which is used to drive the loading system of a mechatronic journal test rig. The mathematical model of the control system is established according to the principle of the electro-hydraulic system. Considering the indetermination of model parameters, the method of parameter identification was used to verify the rationality of the theoretical model. In order to improve the control precision of the hydraulic loading system, the traditional PID controller and fractional-order PID controller are designed by selecting appropriate tuning parameters. Their control performances are analyzed in frequency domain and time domain, respectively. The results show that the fractional-order PID controller has better control effect. By observing the actual control effect of the fractional-order PID controller on the journal test rig, the effectiveness of this control algorithm is verified.

Keywords: electro-hydraulic system; fractional-order PID controller; journal bearing test rig; system identification.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest.

Figures

Figure 1
Figure 1
Principle diagram of hydraulic system.
Figure 2
Figure 2
Control schematic diagram.
Figure 3
Figure 3
Electric-hydraulic proportional relief valve.
Figure 4
Figure 4
Working principle diagram.
Figure 5
Figure 5
Transfer function block diagram.
Figure 6
Figure 6
Dynamic curve diagram of real time data.
Figure 7
Figure 7
System identification contrast diagram.
Figure 8
Figure 8
Simulation model diagram.
Figure 9
Figure 9
Main mechanism of Journal bearing test rig.
Figure 10
Figure 10
Dynamic curve diagram of real time data.
Figure 11
Figure 11
Square wave input signal tracking response.
Figure 12
Figure 12
Sine input signal tracking response.
Figure 13
Figure 13
Bode plots of close loop.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Elbayomy K.M., Jiao Z., Zhang H. PID Controller Optimization by GA and Its Performances on the Electro-Hydraulic Servo Control System. Chin. J. Aeronaut. 2008;21:378–384. doi: 10.1016/S1000-9361(08)60049-7. - DOI
    1. Guan C., Pan S. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters. Control Theory Appl. 2008;16:1275–1284. doi: 10.1016/j.conengprac.2008.02.002. - DOI
    1. Toscano R. A simple robust PI/PID controller design via numerical optimization approach. J. Process Control. 2005;15:81–88. doi: 10.1016/j.jprocont.2004.03.005. - DOI
    1. Mohanty A., Yao B. Indirect Adaptive Robust Control of Hydraulic Manipulators with Accurate Parameter Estimates. IEEE Trans. Control Syst. Technol. 2011;19:567–575. doi: 10.1109/TCST.2010.2048569. - DOI
    1. Yang G., Yao J., Le G., Ma D. Adaptive integral robust control of hydraulic systems with asymptotic tracking. Mechatronics. 2016;40:78–86. doi: 10.1016/j.mechatronics.2016.10.007. - DOI

LinkOut - more resources