A Tutorial for Information Theory in Neuroscience

Abstract

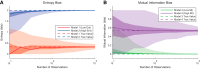
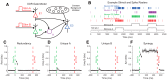
Understanding how neural systems integrate, encode, and compute information is central to understanding brain function. Frequently, data from neuroscience experiments are multivariate, the interactions between the variables are nonlinear, and the landscape of hypothesized or possible interactions between variables is extremely broad. Information theory is well suited to address these types of data, as it possesses multivariate analysis tools, it can be applied to many different types of data, it can capture nonlinear interactions, and it does not require assumptions about the structure of the underlying data (i.e., it is model independent). In this article, we walk through the mathematics of information theory along with common logistical problems associated with data type, data binning, data quantity requirements, bias, and significance testing. Next, we analyze models inspired by canonical neuroscience experiments to improve understanding and demonstrate the strengths of information theory analyses. To facilitate the use of information theory analyses, and an understanding of how these analyses are implemented, we also provide a free MATLAB software package that can be applied to a wide range of data from neuroscience experiments, as well as from other fields of study.

Keywords: Information flow; information theory; mutual information; neural computation; neural encoding; transfer entropy.

Figure 1.

General information theory analysis protocol. A, A neuroscience experiment or simulation is performed to gather environmental data (e.g., stimuli), physiologic data (e.g., voltage recordings), and/or behavioral data (e.g., animal location). B, If necessary, the data are then discretized (see Data Binning). Some types of data (e.g., spike data) do not require discretization. In this example, two sets of data were produced, but analysis of any number of data sets is possible. C, The discretized data are then converted to probability distributions by first counting the number of times each unique set of states was observed. In the case of single trial data (gray tables), the joint states for all of the data are counted to estimate the probability distribution. In the case of trial-based data (green and orange tables), the joint states are counted for all data at certain time bins across trials. D, The desired information theory measure is applied to the probability distribution.

Figure 2.

Example data discretization. A, 200 example data points were randomly generated (vertical black lines represent individual data points, black plot represents a fine-resolution histogram). The data were discretized into four uniform width bins or states (top colored regions) or four uniform count bins or states (bottom colored regions). B,C, The number of data points in each bin divided by the total number of data points was then used as the probability for each bin (state). Uniform width bins (B) can preserve general data distribution features (e.g., two peaks in this case), but produce some bins with low probabilities. Uniform count bins (C) produce uniform probability distributions, which have certain information theory advantages, but do not preserve general data distribution features.

Figure 3.

Example entropy calculations. A, Example probability distributions for three models (red, blue, and green); B, their associated entropy values. Model 1 was most likely to be in state 1, so it had low entropy. Model 3 was equally likely to be in all four states, so it had maximum entropy. Uniform count binning (see Data Binning) will produce equally likely states and maximize entropy, similar to Model 3.

Figure 4.

Example mutual information calculations. A, Example probability distributions for three models (red, blue, and green); B, their associated mutual information values. In model 1, the $X$ and $Y$ variables were independent, so their mutual information was zero. In model 2, knowledge of $X$ or $Y$ reduces our uncertainty in the state of the other variable to some extent, so nonzero mutual information was observed. In model 3, $X$ and $Y$ are identical, so their mutual information was maximal.

Figure 5.

Example of linear versus nonlinear analysis methods. A, Example data for three models (red, blue, and green) with linear (red) and nonlinear (blue and green) interactions; B, the associated correlation coefficient and mutual information (MI) values for all three models (star: p < 0.05, correlation coefficient and p-value calculated via MATLAB, mutual information and p-value calculated via the Neuroscience Information Theory Toolbox; see Data Binning and Significance Testing, 4 bins and 1000 null data sets).

Figure 6.

Example transfer entropy calculations. A, Example model spike trains (color bands: spikes); B, their associated transfer entropy values. Model 1 contained independent neurons, so it produced zero transfer entropy. Models 2 and 3 contained interactions from neuron X to Y. In model 3, neuron X’s state precisely determined neuron Y’s state one time step in the future, which produced maximal transfer entropy. In model 4, neuron X’s state precisely determines neuron Y’s state, but the past of neuron Y also determines its future, so it produced zero transfer entropy.

Figure 7.

Partial information interpretations and example systems. A, Though the partial information decomposition does not require explicit time ordering, it is frequently helpful to apply converging or diverging ordering to the interactions. B, Example of purely redundant systems. The $X$ variables provided the same amount of information about each state of $Y$. C, Example purely synergistic systems. The $X$ variables alone provided no information about $Y$, though they did together via a nonlinear operation (Op). D, Example purely unique systems. In the converging example, only $X_1$ provided information about $Y$. In the diverging example, each $X$ variable provided information about different states of $Y$. The joint probability distributions for these systems are listed as extended data in Fig. 7-1.

Figure 8.

Example bias in entropy and mutual information calculations. A, Distributions of entropy values for low (0.33 bits) and high (2 bits) models as a function of number of observations. Entropy values tended to be biased downwards, though some trials produced elevated entropy values for trials with few observations. The probability distribution models were $p_{low}=\left\{\mathrm{0.95,0.04,0.009,0.001}\right\}$ and $p_{high}=\left\{\mathrm{0.25,0.25,0.25,0.25}\right\}$. The binning method (four total bins) allowed for a maximum entropy of 2 bits. B, Distributions of mutual information values for low (0 bits) and high (0.53 bits) models as a function of number of observations. Mutual information values tended to be biased upwards, though some trials produced lower mutual information values for trials with few observations. Both models had two variables, each with two states. In the low-mutual-information model, all joint states were equally likely (i.e., independent variables). In the high-entropy model, the matching joint states had a probability of 0.45 and the other joint states had a probability of 0.05. The binning method (four total joint states) allowed for a maximum mutual information of 1 bit. Dark fringe represents interquartile range, and light fringe represents extremum range over 1000 trial simulations for each model and each unique number of observations.

Figure 9.

Example significance testing for mutual information via surrogate data null models. A,B, Example histogram of null model (randomized real data) mutual information values and the mutual information value from the real data (red line) for a system with no interactions (A) and for a system with interactions (B). As expected, the p-value in A indicates that the null model ($X$ and $Y$ are independent) cannot not be rejected. In B, the p-value is low enough to reject the null model. C, p-values for models with different numbers of observations as a function of interaction strength (100 models generated for each $a$ value and number of observations, solid line: median, fringe: interquartile range). Larger interaction strengths produced lower p-values, and models with more observations could detect weaker interactions. The minimum p-value resolution available in this demonstration was 0.0001 because 10,000 surrogate data sets were generated for each real data set.

Figure 10.

Single neuron stimulus encoding is captured in a variety of situations. A, Stimulus on versus stimulus off. B, Strong stimulus versus weak stimulus. C, Stimulus delay. D, Nonlinearly filtered stimulus. 1, Explanatory diagrams. 2, Neuron firing rates were modified by the application of a depolarizing square pulse. Blue lines: spikes; A2 and B2 involved the application of a strong stimulus and a zero or weak stimulus, respectively. C2 involved a delay between the application of the stimulus and it being received by the neuron. D2 involved a nonlinear filter of the stimulus that weakened the strongest applied stimulus and strengthened the weakest applied stimulus. 3, Stimulus encoding through time as measured by mutual information between the spike count of the neuron and the stimulus state [(A3 and C3): on/off (B3): strong/weak (D3): weak/medium/strong, dots: mean, error bars: standard deviation across models ($n=20$)]. In all cases, large amounts of mutual information were observed between the spike count and the stimulus state during the stimulus, but not otherwise (accounting for the delay in C).

Figure 11.

Information transmission between neuron peaks at the onset of transmission. A, An excitatory neuron (E1) received a stimulus and then sent current to a second excitatory neuron (E2). B, Both E1 and E2 spiked during the stimulus, though E1 started spiking earlier. C, Mutual information between E2 and the stimulus state (on/off). E2 encoded the spiking state throughout the stimulus. D, Transfer entropy from E1 to E2 peaked immediately following the onset of the stimulus and was nonzero before, during, and after the stimulus. This elevated transfer entropy was due to the constant existence of the connection. E, Information transmission from E1 to E2 about the stimulus state (on/off) peaked at the onset of the stimulus, was nonzero throughout the stimulus, but was near zero otherwise. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 12.

Inhibition can modulate stimulus encoding modalities. A, Excitatory neuron E1 received stimulus current and sent current to inhibitory neuron I1 and excitatory neuron E2. Neuron I1 also inhibited neuron E2. B, Average mutual information during stimulus between the spike count of E2 and the stimulus state (on/off) as a function of inhibition current from I1 to E2. Note the local maxima in encoding for low inhibition and high inhibition. Also, note that mutual information is able to detect both firing rate increases and decreases, though firing rate decreases provide less information. C, Average mutual information during stimulus between the stimulus state (on/off) as a function of inhibition current from I1 to E2 for E1 alone and for I1 and E2 jointly. Note that I1 and E2 jointing encoded the stimulus state for all inhibition levels better than E1 alone, despite the fact that only E1 received the stimulus current. D, Weak inhibition. E, Medium inhibition. F, Strong inhibition. (1) Example spike rasters. (2) Mutual information between the stimulus state (on/off) and neuron E2. (3) Mutual information between the stimulus state (on/off) and E1 alone or I1 and E2 jointly. In D, neuron E2 encoded the stimulus state by increasing firing during the stimulus on state. In E, the inhibition and excitation balanced to render neuron E2’s firing rate unchanged by the stimulus. In F, neuron E2 encoded the stimulus state by decreasing firing during the stimulus on state. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 13.

Activity waves carry stimulus information and transmit information. A, Example 1000 neuron Izhikevich network on a 2-D surface with periodic boundary conditions and distance dependent connectivity. 40 neurons near the center line were stimulated. Only connections from stimulated neurons are shown to improve clarity (gray lines). B, Example spike raster sorted by distance from the x = 0.5 line. Following the application of the stimulus, a wave of activity propagated outwards from the center. C, Average mutual information across all models ($n=20$) between the stimulus state (on/off) and the neurons as a function of neuron position. Note that the encoding spreads outwards from the center line of the network. D, Example transfer entropy between neurons as a function of time from stimulus. The nonstimulus neurons are sorted by distance from the line x = 0.5. Note that transfer entropy first appears from stimulated neurons to nearby nonstimulated neurons (5–10 ms), then appears from nearby nonstimulated neurons to more distant neurons (10–15 ms).

Figure 14.

Unique information represents encoding about one stimulus in a joint set. A, Excitatory neuron E1 received input current from stimulus A, while excitatory neuron E2 received input current from stimulus B. Only E1 sent current to excitatory neuron E3. B, Example spike raster with stimuli. As expected, stimulus A caused neuron E1 to fire, which caused neuron E3 to fire. C–F, PID values between the spike count of E3 and the stimuli states (on/off). Neuron E3 encoded only the state of stimulus A, so E3 uniquely encoded stimulus A. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 15.

Synergy represents encoding simultaneous information about both stimuli. A, Neuron E3 received excitatory inputs from neurons E1 and E2, both of which received stimulation. Neurons E1 and E2 also sent current to inhibitory neuron I1, which inhibited E3. Neuron E3 also received constant background inhibition from other neurons. B, Example spike rasters. Neurons E1 and E2 fired when their respective stimulus is applied. Note that neuron E3 only fired when either E1 or E2 was active, but not both due to inhibition from I1. C–F, PID values between the spike count of E3 and the stimuli states (on/off). Neuron E3 showed sustained synergy because it encoded information about the simultaneous states of stimuli A and B. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 16.

Varying background activity can produce NOR-Gate like activity and modulate redundancy and synergy. A1,B1, Inhibitory neurons I1 and I2 received unique stimuli and inhibited neuron E1. In A1, neuron E1 also received background constant excitation, but not in B1. A2,B2, Example spike rasters. In A2, the background excitation made E1 perform a NOR operation (E1 fired when neither A nor B is on). C–F, PID values between the spike count of E1 and the stimuli states (on/off). Neuron E1 showed sustained synergy and redundancy with the background excitation on, but little encoding with background excitation off. Synergy and redundancy were observed because the encoding provided simultaneous information about both stimuli for some cases, but not all cases. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 17.

Input correlation affects synergy and redundancy. A, Excitatory neurons E1 and E2 received stimuli and sent current to neuron E3. B, The correlation between the stimuli can be modulated by the parameter $a$ ($a=-0.25$ implies anticorrelation, $a=0$ implies uncorrelated, and $a=0.25$ implies correlation). C, Example spike raster in the uncorrelated case (all four stimuli combinations are equally likely). Note that the correlation affected the number of times each stimuli pattern is observed, but not the spiking activity that resulted from a given stimulation pattern. PID redundancy (D) and synergy (E) between neuron E3 spike count and the stimuli state. 1, Anticorrelated stimuli. 2, Uncorrelated stimuli. 3, Correlated stimuli. 4, Average information value during stimulation as a function of correlation parameter $a$. In the anticorrelated case, neuron E3 did not encode the stimuli. In the uncorrelated case, both synergy and redundancy were present. In the correlated case, only redundancy was present. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 18.

PID reveals redundant and synergistic encoding at activity wave collision points. A, Example 1000 neuron Izhikevich network on a 2-D surface with periodic boundary conditions and distance dependent connectivity. 40 neurons near the line x = 0.25 (x = 0.75) received stimulus A (B). Only connections from stimulated neurons are shown to improve clarity (gray lines). B, Example spike rasters sorted by x position. Following the application of stimulus, a wave of activity propagated outwards from the stimulation points. (No stimulus spike rasters not shown.) C,D, Average PID values across all models ($n=20$) between the spike count of each neuron and the stimuli states (on/off) as a function of location. Neurons closest to the stimulation lines showed large amounts of unique encoding for the corresponding stimulus (C and D). Neurons between the stimulus locations (where the activity waves collided) showed high levels of synergy and redundancy (E and F).

Figure 19.

Habituated motor neuron encodes stimulus type and number. A, A sensory neuron (S) was stimulated and sent current to a motor neuron (M). The strength of the synapse weakened with repeated stimulation of S. B, Example spike rasters. In the first trial, stimulation of the sensory neuron caused elevated spiking of the sensory neuron and the motor neuron. However, by the last trial, stimulation of the sensory neuron caused elevated spiking of only the sensory neuron. C,D, Mutual information between a neuron’s spike count and the stimulus state. The weakening synapse caused weaker encoding by the motor neuron, though it did still encode the stimulus. E,F, Mutual information between a neuron’s spike count and the trial number (e.g., early/late). Because the motor neuron’s activity changed with trial, the motor neuron encoded the trial number. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 20.

Model center-surround retinal ganglion cells jointly encode stimulus location synergistically and redundantly. A, Example receptive field for a neuron in a 2-D plane with periodic boundary conditions showing stimulation locations that increase (+), decrease (–), or do not change the firing of the neuron. B, Example spike rasters for the stimuli and receptive field shown in A. Stim 1 occurred in the center of the receptive field and increased firing. Stim 2 occurred in the periphery of the receptive field and decreased firing. Stim 3 occurred outside the receptive field and did not affect firing. C, Mutual information between the stimulus location and the spike count of an example neuron from each model [receptive field in A; dots: mean, error bars: standard deviation across models ($n=20$)] D, PID values between neuron spike counts and the location of the stimulus for pairs of neurons as a function of the distance between the centers of the receptive fields of the neurons. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)]. Note that redundancy was maximized for overlapping receptive fields, unique information peaked for neighboring place fields, and synergy peaked for concentric receptive fields. Furthermore, synergy values were substantially higher than redundancy indicating that synergy dominates joint encoding in this system.

Figure 21.

Model primary motor cortex neurons jointly encode movement direction. A, Possible directions of motion. B, Example firing rate profiles for a strong direction encoder (B1) and a weak direction encoder (B2). C, Maximum mutual information between the direction of motion and the spike count of a neuron as a function of the strength of neuron response to direction. D, Example mutual information between the direction of motion and the spike count of the neuron for the corresponding examples from (B). E–H, PID values between the spike count of pairs of neurons and the direction of motion as a function of the difference in preferred firing angle between the neurons for only strong encoders ($r=1$). Note, elevated redundancy was observed for parallel and antiparallel preferred firing angles, while elevated unique information was observed for perpendicular preferred firing angles. Synergy was relatively constant for all angle differences. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)].

Figure 22.

Joint encoding by model place cells is distance dependent. A, A model animal was allowed to randomly walk on a 2-D surface with periodic boundary conditions. B, Example animal linger time as a function of position. C, An example place cell shows elevated firing when the animal was near its place field (white circle). D, Place cells encoded the location of the animal better than nonplace cells that did not respond to location. (Thin bars: min to max range, thick bars: interquartile range, rank-sum test, p < 0.001.) E, PID values between neuron spike counts and the location of the animal for pairs of neurons as a function of the distance between the centers of the place fields of the neurons. [For all information plots, dots: mean, error bars: standard deviation across models ($n=20$)]. Note that redundancy was maximized for overlapping place fields, unique information peaked for neighboring place fields, and synergy was elevated regardless of the relative positions of the neurons.