Expanding the Active Inference Landscape: More Intrinsic Motivations in the Perception-Action Loop

Abstract

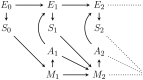
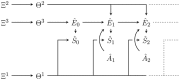
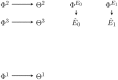
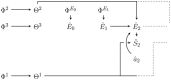
Active inference is an ambitious theory that treats perception, inference, and action selection of autonomous agents under the heading of a single principle. It suggests biologically plausible explanations for many cognitive phenomena, including consciousness. In active inference, action selection is driven by an objective function that evaluates possible future actions with respect to current, inferred beliefs about the world. Active inference at its core is independent from extrinsic rewards, resulting in a high level of robustness across e.g., different environments or agent morphologies. In the literature, paradigms that share this independence have been summarized under the notion of intrinsic motivations. In general and in contrast to active inference, these models of motivation come without a commitment to particular inference and action selection mechanisms. In this article, we study if the inference and action selection machinery of active inference can also be used by alternatives to the originally included intrinsic motivation. The perception-action loop explicitly relates inference and action selection to the environment and agent memory, and is consequently used as foundation for our analysis. We reconstruct the active inference approach, locate the original formulation within, and show how alternative intrinsic motivations can be used while keeping many of the original features intact. Furthermore, we illustrate the connection to universal reinforcement learning by means of our formalism. Active inference research may profit from comparisons of the dynamics induced by alternative intrinsic motivations. Research on intrinsic motivations may profit from an additional way to implement intrinsically motivated agents that also share the biological plausibility of active inference.

Keywords: active inference; empowerment; free energy principle; intrinsic motivation; perception-action loop; predictive information; universal reinforcement learning; variational inference.

Figure 1

First two time steps of the Bayesian network representing the perception-action loop (PA-loop). All subsequent time steps are identical to the one from time t = 1 to t = 2.

Figure 2

Bayesian network of the generative model with parameters Θ = (Θ¹, Θ², Θ³) and hyperparameters Ξ = (Ξ¹, Ξ², Ξ³). Hatted variables are models / estimates of non-hatted counterparts in the perception-action loop in Figure 1. An edge that splits up connecting one node to n nodes (e.g., Θ² to Ê₁, Ê₂, …) corresponds to n edges from that node to all the targets under the usual Bayesian network convention. Note that in contrast to the perception-action loop in Figure 1, imagined actions Â_t have no parents. They are either set to past values or, for those in the future, a probability distribution over them must be assumed.

Figure 3

Internal generative model with plugged in data up to t = 2 with Ŝ₀ = s₀, Ŝ₁ = s₁ and Â₁ = a₁ as well as from now on fixed hyperparameters ξ = (ξ¹, ξ², ξ³). Conditioning on the plugged in data leads to the posterior distribution $q({ŝ}_{t:\widehat{T}},{ê}_{0:\widehat{T}},{â}_{t:\widehat{T}},\theta |s{a}_{\prec t},\xi )$. Predictions for future sensor values can be obtained by marginalising out other random variables e.g., to predict Ŝ₂ we would like to get q(ŝ₂|s₀, s₁, a₁, ξ). Note however that this requires an assumption for the probability distribution over Â₂.

Figure 4

Bayesian network of the approximate posterior factor at t = 2. The variational parameters Φ¹, Φ², Φ³, and ${\Phi }^{E_{\prec t}}=({\Phi }^{E_0},{\Phi }^{E_1})$ are positioned so as to indicate what dependencies and nodes they replace in the generative model in Figure 2.

Figure 5

Bayesian network of the approximate complete posterior of Equation (40) at t = 2 for the future actions ${â}_{t:\widehat{T}}$. Only ${Ê}_{t-1},{\Theta }^1,{\Theta }^2$ and the future action ${â}_{t:\widehat{T}}$ appear in the predictive factor and influence future variables. In general there is one approximate complete posterior for each possible sequence ${â}_{t:\widehat{T}}$ of future actions.

Figure 6

Generative model including $q({â}_{t:\widehat{T}}|s{a}_{\prec t},\xi )$ at t = 2 with ŜÂ_≺2 influencing future actions ${Â}_{2:\widehat{T}}$. Note that, only future actions are dependent on past sensor values and actions, e.g., action Â₁ has no incoming edges. The increased gap between time step t = 1 and t = 2 is to indicate that this time step is special in the model. For each time step t there is an according model with the particular relation between past ŜÂ_≺t and ${Â}_{t:\widehat{T}}$ shifted accordingly.