Putting the "dynamic" back into dynamic functional connectivity

Abstract

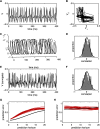
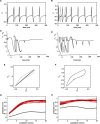
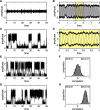
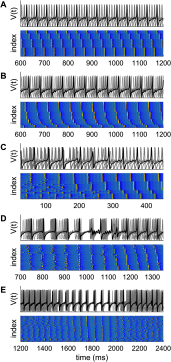
The study of fluctuations in time-resolved functional connectivity is a topic of substantial current interest. As the term "dynamic functional connectivity" implies, such fluctuations are believed to arise from dynamics in the neuronal systems generating these signals. While considerable activity currently attends to methodological and statistical issues regarding dynamic functional connectivity, less attention has been paid toward its candidate causes. Here, we review candidate scenarios for dynamic (functional) connectivity that arise in dynamical systems with two or more subsystems; generalized synchronization, itinerancy (a form of metastability), and multistability. Each of these scenarios arises under different configurations of local dynamics and intersystem coupling: We show how they generate time series data with nonlinear and/or nonstationary multivariate statistics. The key issue is that time series generated by coupled nonlinear systems contain a richer temporal structure than matched multivariate (linear) stochastic processes. In turn, this temporal structure yields many of the phenomena proposed as important to large-scale communication and computation in the brain, such as phase-amplitude coupling, complexity, and flexibility. The code for simulating these dynamics is available in a freeware software platform, the Brain Dynamics Toolbox.

Keywords: Dynamic functional connectivity; Metastability; Multistability; Nonlinear dynamics.

Figure 1.. Uncoupled systems. (A) Time series for two uncoupled neural masses (V₁ is black, V₂ is gray) in the chaotic regime. (B) The same time series with V₁ plotted against V₂. Transients (t < 100) have been omitted. (C) Hilbert phase of V₁ relative to V₂. Plotted in cylindrical coordinates with unit radius. (D) Distribution of linear correlations between V₁ and V₂ for multiple simulation runs with random initial conditions. (E) Amplitude-adjusted surrogates for the time series from panel A. (F) Distribution of linear correlations between surrogate data drawn from the same instances of V₁ and V₂ (i.e., one simulation run, multiple shuffles of the surrogate data). (G) Nonlinear self-prediction of V1 from itself (black) and from surrogate data (red). Note that both errors grow toward one with longer prediction horizons, but the original data falls well below the null distribution. (H) Nonlinear cross-prediction of V₁ from V₂ (black) and from surrogate data (red). Here the empirical data falls within the surrogate distribution, reflecting the absence of intersystem coupling.

Figure 2.. Generalized synchrony. (A) Time series for two coupled identical neural masses (V₁ is black, V₂ is gray) exhibiting identical synchronization. (B) Time series for two coupled nonidentical neural masses (V₁ is black, V₂ is gray) exhibiting generalized synchronization. (C) Hilbert phase of V₁ relative to V₂ for the case of identical synchronization. Note the rapid approach to stable 1:1 phase synchrony. (D) Hilbert phase of V₁ relative to V₂ for the case of generalized synchronization. Brief, but incomplete, phase slips continue to occur following the transient. (E) V₁ plotted against V₂ for the cases of identical synchronization. After a brief transient, the system approaches the diagonal. (F) V₁ plotted against V₂ for the cases of generalized synchronization. Transients have been omitted. (G) Nonlinear self-prediction of V₁ from itself (black) and from surrogate data (red). (H) Nonlinear cross-prediction of V₁ from V₂ (black) and from surrogate data (red).

Figure 3.. Metastability. (A) Time series for two weakly coupled neural masses (V₁ is black, V₂ is gray) showing a single instance of desynchronization. (B) Hilbert phase of V₁ relative to V₂ with relatively weak coupling. Periods of generalized synchronization are interspersed by erratic desynchronization. The gray shaded region (bottom of panel) shows the point-wise correlations between V₁(t) and V₂(t) smoothed over a 1-s moving window. (C) Hilbert phase of V₁ relative to V₂ with medium coupling. The instances of desynchronization have become relatively infrequent and briefer. (D) With strong coupling, instances of desynchronization are relatively rare. (E) Plot of V₁ versus V₂ for the case of strong coupling. The desynchronization is seen as a brief, erratic excursion from the synchronization manifold. (F) Nonlinear self-predictions of V₁ from itself (black), and (G) nonlinear cross-predictions of V₁ from V₂ (black). Predictions of V₁ from surrogate versions of V₂ are shown in red. The time series retain nonlinear structure despite the instances of desynchronization.

Figure 4.. Multistability. (A) Time series of the noisy subcritical Hopf model with one node. With β = −10 the system exhibits a stable (noise perturbed) fixed point at r = 0. (B) With β = −6 the system exhibits a stable limit cycle with amplitude r = 2. Oscillations are shown in gray. Black represents the noise-driven amplitude fluctuations, with close-up shown in panel D. (C) With β = −7.5, the system exhibits bistability with noise-driven switching between the fixed point and limit cycle. For simplicity, the (gray) oscillations are not shown. (E) System with two nodes and β = −7.5 but zero coupling (c = 0). The systems jump between the fixed point and limit cycles independently. (F) Histogram of the linear correlations between the time series generated by the two nodes from panel E. The simulation was repeated for N = 200 trials with random initial conditions for each trial. The correlations center at 0 but with substantial intertrial variability. (G) System with two nodes and β = −7.5 and strong coupling (c = 1). The jumps between the fixed point and limit cycles occur in similar time windows. (F) Histogram of the linear correlations between the time series generated by the two nodes from panel E. The correlations center well above 0 with reduced intertrial variability.

Figure 5.. Complex dynamics in larger ensembles. (A) Stable partitioning of ensemble dynamics into four phase-coupled clusters with τ = 10 ms and coupling c = 0.75. (B) Partitioning of ensemble dynamics into six phase-coupled clusters with τ = 6 ms and coupling c = 0.75. There is slightly greater disorder in some of the clusters compared with those in panel A. (C, D) With weaker coupling and/or shorter time delays (τ = 5.5 ms, c = 0.45), there are brief phase slips, leading to a reorganization of the cluster configuration. (E) With briefer time delays (τ = 5 ms), clustering does not occur. Instead the system shows instances of global synchrony interspersed among spatiotemporal chaos.