Nonreciprocal responses from non-centrosymmetric quantum materials

Abstract

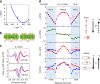
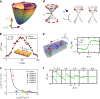
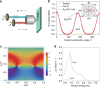
Directional transport and propagation of quantum particle and current, such as electron, photon, spin, and phonon, are known to occur in the materials system with broken inversion symmetry, as exemplified by the diode in semiconductor p-n junction and the natural optical activity in chiral materials. Such a nonreciprocal response in the quantum materials of noncentrosymmetry occurs ubiquitously when the time-reversal symmetry is further broken by applying a magnetic field or with spontaneous magnetization, such as the magnetochiral effect and the nonreciprocal magnon transport or spin current in chiral magnets. In the nonlinear regime responding to the square of current and electric field, even a more variety of nonreciprocal phenomena can show up, including the photocurrent of topological origin and the unidirectional magnetoresistance in polar/chiral semiconductors. Microscopically, these nonreciprocal responses in the quantum materials are frequently encoded by the quantum Berry phase, the toroidal moment, and the magnetoelectric monopole, thus cultivating the fertile ground of the functional topological materials. Here, we review the basic mechanisms and emergent phenomena and functions of the nonreciprocal responses in the noncentrosymmetric quantum materials.

Fig. 1

Magnetochiral dichroism and gyrotropic birefringence (GB) in multiferroics. a Schematic illustration of the conical screw spin structure under an external magnetic field (H_ex) in multiferroic CuFe_1–xGa_xO₂ (x = 0.035). The H_ex parallel to the in-plane magnetic modulation q_m (e.g., // [110]) modifies the proper screw spin structure to the conical one. The ferroelectric polarization (P) driven by the screw spin structure also points to the in-plane q_m direction ([110]). The electromagnon spectra of (b) real part n(ω) and (c) imaginary part κ(ω) of the complex refractive index at 4.6 K and 7 T (H_ex || [110]) with the light configuration in (a). Spectra with both signs of spin helicity (γ_m( + ) or γ_m(–)) and magnetization ( +M or –M) are shown. In the respective lower panels, magnetoelectric spectra are shown defined as (b) Δn(ω) = n( + k^ω)–n(–k^ω) and (c) Δk(ω) = κ(+k^ω) –κ(– k^ω). d Schematic of GB for light with propagation vector + k^ω (upper) and −k^ω (bottom) perpendicular to the c axis in the case of (Fe; Zn)₂Mo₃O₈; P_s and M_s stand for the spontaneous electric polarization and magnetization. P^ω and P_ME show the electric polarizations induced by the electric field (E^ω) and magnetic field (B^ω) of light, respectively. The green plate and red and blue bars denote the sample and rotating principal optical axes, respectively. Reprinted figure with permission from ref. Copyright (2017) by the American Physical Society. e Axion insulator potentially showing the topological magnetoelectric effect and associated GB, composed of the magnetic topological insulator with the opposite magnetization directions on the top and bottom layers. Figure from ref. with permission from Nature Publishing Group

Fig. 2

Spin wave spectroscopy on the nonreciprocal magnon transport in a chiral magnet. a Asymmetric spin wave dispersions for the collinear ferromagnetic state in a chiral magnet MnSi according to Eq. (3); a sharp spike around k~0 is due to the dipolar interaction. b The experimental setup to detect the nonreciprocity for the magnon transport between the coplanar microwave guides (ports 1 and 2). c Imaginary part spectra of the mutual inductance ΔL₁₂ (ΔL₂₁), representing the transport of the magnons from 1 to 2 (from 2 to 1) for magnetic fields applied parallel (+H) or antiparallel (–H) to the propagation direction; the result for the enantiomer D-body crystal. Another enantiomer L-body crystal shows the opposite behaviors for the exchange between ΔL₁₂ and ΔL₂₁. d Magnetic field dependence of spin wave nonreciprocity between ΔL₁₂ and ΔL₂₁ (i.e., +k and −k), measured for the D-body crystal of Cu₂OSeO₃ with the H // k // [001] configuration at 30 K. Here, ν_p indicates the magnetic resonance frequency giving the peak value of |ΔLnm|, and Δν_p the difference between ±k, respectively. |ΔL^p_nm | and v^p_g indicate the corresponding peak value and the group velocity at the frequency ν_p. The right panel shows the schematic illustration of collinear ferromagnetic state and helical spin state, respectively. The nonreciprocal spin wave propagation between ±k is discerned only in the former spin state. Reprinted figure with permission from ref. Copyright (2016) by the American Physical Society

Fig. 3

Systems showing the unidirectional magnetoresistance. There are two classes according to the crystal symmetry, i.e., polar and chiral structures. Polar systems include Si FET, magnetic bilayer, BiTeBr, and surface state of topological insulator (TI). In this class of systems, the resistivity R showing the magnetochiral anisotropy has the form R = R₀[1+γ(P×B)·I] where the directions of the polarization P, magnetic field B, and the current I (electric field E) are orthogonal to each other. There are several microscopic mechanisms of the magnetochiral anisotropy. For Si FET, the relativistic Lorentz transformation and associated correction due to the factor v/c (v: velocity of electrons, c: velocity of light) was proposed. For magnetic bilayer Ta|Co and Pt|Co systems, it has been proposed that the current-induced spin accumulation modifies the resistivity through the spin–orbit interaction and spin-dependent scattering. The asymmetric band dispersion under the in-plane magnetic field in the presence of the Rashba spin–orbit interaction is identified as the origin of the nonreciprocal resistivity in BiTeBr, while the asymmetric scattering of electrons by magnons is the origin in the surface state of topological insulator (TI). The examples of the other class, i.e., the chiral structure, are shown in the lower part, which shows the behavior R = R₀[1+γ(B·I)] called the electrical magnetochiral effect. Examples of this class include Bi helix^,, molecular solid, and MiSi. The helix structure is a representative example of this class. It has been discussed that the magnetic field b produced by the current is combined to the external magnetic field B, and the magnetoresistance for b + B results in the electrical magnetochiral effect in Bi helix. Similar effect was also observed in a molecular semiconductor [DM-EDT-TTF]₂ClO₄ (middle of the lower panel). In a ferromagnet, the time-reversal symmetry is spontaneously broken, and the chiral ferromagnet can show the electrical magnetochiral effect. MnSi is a representative example, and that effect is enhanced above the helical transition temperature T_c. This suggests that the spin fluctuation of chiral nature is the origin of the electrical magnetochiral effect. Reprinted figures with permission from ref^,,. Copyright (2001, 2005, 2016) by the American Physical Society. Figures from ref.^–,, with permission from Nature Publishing Group

Fig. 4

Magnetochiral anisotropy in polar systems. a The distorted band structure of Rashba system under the external magnetic field. When the polar axis is along the c-direction, the spin splitting occurs with the spin polarization for each band lying in the a–b plane. When the magnetic field is applied along b axis, the asymmetry between two directions along a-axis appears. b The dependence of the nonlinear resistivity corresponding to the γ term in Eq. (B1) on the direction of the external magnetic field in BiTeBr, which is consistent with the formula R = R₀[1+γ′(P × B)·I]. c The coefficient γ as a function of electron density in BiTeBr. The black curve is the theoretical calculation without any fitting parameters. Figure from ref. Reprinted with permission from Nature Publishing Group. d Schematics of the surface state of a three-dimensional topological insulator, which is described by the two-dimensional Weyl Hamiltonian with spin-momentum locking. With the in-plane magnetization along the y-axis, the inelastic scattering due to magnons to the right and left directions is different, leading to the nonreciprocal transport. e The schematic experimental setup (left), and the obtained magnetic field dependence of the nonlinear resistivity. f Magnetic field dependence of nonlinear resistivity at several temperatures. Reprinted figure with permission from ref. Copyright (2016) by the American Physical Society

Fig. 5

Second-harmonic (SH) generation from the toroidal moments in multiferroics. a Crystal and magnetic structures of GaFeO₃. In the right panel, outward (inward) arrows represent the spin direction of Fe1 (Fe2) atoms antiparallel (parallel) to the c axis. Horizontal solid lines represent the shifted positions of Fe ions along the b axis from the symmetric positions (dashed lines) of FeO₆ octahedra. Note that the shifted directions of Fe1 and Fe2 atoms are opposite to each other. Reprinted figure with permission from ref. Copyright (2005) by the Physical Society of Japan. b Experimental configuration for the measurement of the Kerr rotation of SH light in a GaFeO₃ crystal (left panel). Analyzer-angle dependence of SH intensity at 180 K (<T_C). Analyzer angles θ of 0 and 90° stand for p- and s-polarized SH light, respectively. Solid and open circles indicate the SH intensity for +z and –z directions of the magnetic field, respectively. c (Left) topographic image of the ac surface of the GaFeO₃ crystal as taken by the SH light in the nonmagnetic configuration, i.e., Pin-Pout. Magnetic domains aligned along the c axis were observed by reflected SH intensity in (center) S_in(S + P)_out and (right) S_in(S–P)_out configurations. Reprinted figure with permission from ref. Copyright (2004) by the American Physical Society

Fig. 6

Second-harmonic generation (SHG) in TaAs. a Schematic of the SHG experimental setup. b SHG intensity as a function of angle of incident polarization at 20 K. c Color plot of the momentum-resolved contribution to the SHG for a model for a simplified mode for TaAs. d The photon-energy dependence of SHG for a simplified model. Figures from ref. Reprinted with persmission from Nature Publishing Group