Preparation of quantum information encoded on three-photon decoherence-free states via cross-Kerr nonlinearities
- PMID: 30218095
- PMCID: PMC6138704
- DOI: 10.1038/s41598-018-32137-3
Preparation of quantum information encoded on three-photon decoherence-free states via cross-Kerr nonlinearities
Abstract
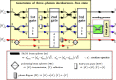
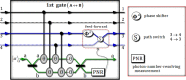
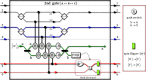
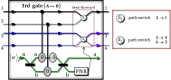
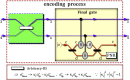
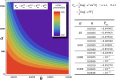
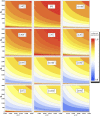
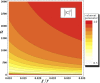
We present a scheme to encode quantum information (single logical qubit information) into three-photon decoherence-free states, which can conserve quantum information from collective decoherence, via nonlinearly optical gates (using cross-Kerr nonlinearities: XKNLs) and linearly optical devices. For the preparation of the decoherence-free state, the nonlinearly optical gates (multi-photon gates) consist of weak XKNLs, quantum bus (qubus) beams, and photon-number-resolving (PNR) measurement. Then, by using a linearly optical device, quantum information can be encoded on three-photon decoherence-free state prepared. Subsequently, by our analysis, we show that the nonlinearly optical gates using XKNLs, qubus beams, and PNR measurement are robust against the decoherence effect (photon loss and dephasing) in optical fibers. Consequently, our scheme can be experimentally implemented to efficiently generate three-photon decoherence-free state encoded quantum information, in practice.
Conflict of interest statement
The authors declare no competing interests.
Figures


Similar articles
-
Scheme for generation of three-photon entangled W state assisted by cross-Kerr nonlinearity and quantum dot.Sci Rep. 2019 Jul 12;9(1):10151. doi: 10.1038/s41598-019-46231-7. Sci Rep. 2019. PMID: 31300664 Free PMC article.
-
Procedure via cross-Kerr nonlinearities for encoding single logical qubit information onto four-photon decoherence-free states.Sci Rep. 2021 May 17;11(1):10423. doi: 10.1038/s41598-021-89809-w. Sci Rep. 2021. PMID: 34001956 Free PMC article.
-
Implementation of SWAP test for two unknown states in photons via cross-Kerr nonlinearities under decoherence effect.Sci Rep. 2019 Apr 16;9(1):6167. doi: 10.1038/s41598-019-42662-4. Sci Rep. 2019. PMID: 30992536 Free PMC article.
-
Distribution of hybrid entanglement and hyperentanglement with time-bin for secure quantum channel under noise via weak cross-Kerr nonlinearity.Sci Rep. 2017 Aug 31;7(1):10208. doi: 10.1038/s41598-017-09510-9. Sci Rep. 2017. PMID: 28860529 Free PMC article.
-
Ultrafast optical control of individual quantum dot spin qubits.Rep Prog Phys. 2013 Sep;76(9):092501. doi: 10.1088/0034-4885/76/9/092501. Epub 2013 Sep 4. Rep Prog Phys. 2013. PMID: 24006335 Review.
Cited by
-
Encoding scheme using quantum dots for single logical qubit information onto four-photon decoherence-free states.Sci Rep. 2020 Sep 18;10(1):15334. doi: 10.1038/s41598-020-71072-0. Sci Rep. 2020. PMID: 32948781 Free PMC article.
-
Scheme for generation of three-photon entangled W state assisted by cross-Kerr nonlinearity and quantum dot.Sci Rep. 2019 Jul 12;9(1):10151. doi: 10.1038/s41598-019-46231-7. Sci Rep. 2019. PMID: 31300664 Free PMC article.
-
Procedure via cross-Kerr nonlinearities for encoding single logical qubit information onto four-photon decoherence-free states.Sci Rep. 2021 May 17;11(1):10423. doi: 10.1038/s41598-021-89809-w. Sci Rep. 2021. PMID: 34001956 Free PMC article.
-
Implementation of SWAP test for two unknown states in photons via cross-Kerr nonlinearities under decoherence effect.Sci Rep. 2019 Apr 16;9(1):6167. doi: 10.1038/s41598-019-42662-4. Sci Rep. 2019. PMID: 30992536 Free PMC article.
References
-
- Bouwmeester D, et al. Experimental quantum teleportation. Nature. 1997;390:575. doi: 10.1038/37539. - DOI
-
- Zeng GH, Keitel CH. Arbitrated quantum-signature scheme. Phys. Rev. A. 2002;65:042312. doi: 10.1103/PhysRevA.65.042312. - DOI
-
- Heo J, et al. Bidirectional transfer of quantum information for unknown photons via cross-Kerr nonlinearity and photon-number-resolving measurement. Chin. Phys. B. 2016;25:020306. doi: 10.1088/1674-1056/25/2/020306. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

