Synchronized mechanical oscillations at the cell-matrix interface in the formation of tensile tissue
- PMID: 30237286
- PMCID: PMC6176648
- DOI: 10.1073/pnas.1801759115
Synchronized mechanical oscillations at the cell-matrix interface in the formation of tensile tissue
Abstract
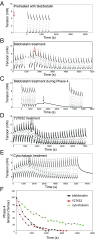
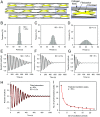
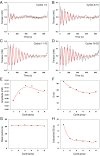
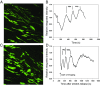
The formation of uniaxial fibrous tissues with defined viscoelastic properties implies the existence of an orchestrated mechanical interaction between the cytoskeleton and the extracellular matrix. This study addresses the nature of this interaction. The hypothesis is that this mechanical interplay underpins the mechanical development of the tissue. In embryonic tendon tissue, an early event in the development of a mechanically robust tissue is the interaction of the pointed tips of extracellular collagen fibrils with the fibroblast plasma membrane to form stable interface structures (fibripositors). Here, we used a fibroblast-generated tissue that is structurally and mechanically matched to embryonic tendon to demonstrate homeostasis of cell-derived and external strain-derived tension over repeated cycles of strain and relaxation. A cell-derived oscillatory tension component is evident in this matrix construct. This oscillatory tension involves synchronization of individual cell forces across the construct and is induced in each strain cycle by transient relaxation and transient tensioning of the tissue. The cell-derived tension along with the oscillatory component is absent in the presence of blebbistatin, which disrupts actinomyosin force generation of the cell. The time period of this oscillation (60-90 s) is well-defined in each tissue sample and matches a primary viscoelastic relaxation time. We hypothesize that this mechanical oscillation of fibroblasts with plasma membrane anchored collagen fibrils is a key factor in mechanical sensing and feedback regulation in the formation of tensile tissues.
Keywords: cell force; collagen; electron microscopy; fibroblast; tension.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

Similar articles
-
The initiation of embryonic-like collagen fibrillogenesis by adult human tendon fibroblasts when cultured under tension.Biomaterials. 2010 Jun;31(18):4889-97. doi: 10.1016/j.biomaterials.2010.02.062. Epub 2010 Mar 30. Biomaterials. 2010. PMID: 20356622 Free PMC article.
-
Tension is required for fibripositor formation.Matrix Biol. 2008 May;27(4):371-5. doi: 10.1016/j.matbio.2007.11.006. Epub 2008 Feb 9. Matrix Biol. 2008. PMID: 18262777
-
Fibronectin matrix polymerization increases tensile strength of model tissue.Am J Physiol Heart Circ Physiol. 2004 Jul;287(1):H46-53. doi: 10.1152/ajpheart.00859.2003. Epub 2004 Mar 4. Am J Physiol Heart Circ Physiol. 2004. PMID: 15001442
-
Cellular control of connective tissue matrix tension.J Cell Biochem. 2013 Aug;114(8):1714-9. doi: 10.1002/jcb.24521. J Cell Biochem. 2013. PMID: 23444198 Free PMC article. Review.
-
Collagen structure of tendon relates to function.ScientificWorldJournal. 2007 Mar 30;7:404-20. doi: 10.1100/tsw.2007.92. ScientificWorldJournal. 2007. PMID: 17450305 Free PMC article. Review.
Cited by
-
Amino acids integrate behaviors in nerveless placozoans.Front Neurosci. 2023 Apr 13;17:1125624. doi: 10.3389/fnins.2023.1125624. eCollection 2023. Front Neurosci. 2023. PMID: 37123368 Free PMC article.
-
Accounting for Material Changes in Decellularized Tissue with Underutilized Methodologies.Biomed Res Int. 2021 May 31;2021:6696295. doi: 10.1155/2021/6696295. eCollection 2021. Biomed Res Int. 2021. PMID: 34159202 Free PMC article. Review.
-
Engineering Biomaterials and Approaches for Mechanical Stretching of Cells in Three Dimensions.Front Bioeng Biotechnol. 2020 Oct 14;8:589590. doi: 10.3389/fbioe.2020.589590. eCollection 2020. Front Bioeng Biotechnol. 2020. PMID: 33154967 Free PMC article. Review.
-
Emergent Temporal Signaling in Human Trabecular Meshwork Cells: Role of TRPV4-TRPM4 Interactions.Front Immunol. 2022 Mar 31;13:805076. doi: 10.3389/fimmu.2022.805076. eCollection 2022. Front Immunol. 2022. PMID: 35432302 Free PMC article.
-
Basic Structure, Physiology, and Biochemistry of Connective Tissues and Extracellular Matrix Collagens.Adv Exp Med Biol. 2021;1348:5-43. doi: 10.1007/978-3-030-80614-9_2. Adv Exp Med Biol. 2021. PMID: 34807414
References
-
- Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. - PubMed
-
- Cameron AR, Frith JE, Cooper-White JJ. The influence of substrate creep on mesenchymal stem cell behaviour and phenotype. Biomaterials. 2011;32:5979–5993. - PubMed
-
- Cameron AR, Frith JE, Gomez GA, Yap AS, Cooper-White JJ. The effect of time-dependent deformation of viscoelastic hydrogels on myogenic induction and Rac1 activity in mesenchymal stem cells. Biomaterials. 2014;35:1857–1868. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

