Estimating Attractor Reachability in Asynchronous Logical Models

Abstract

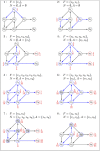
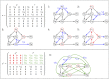
Logical models are well-suited to capture salient dynamical properties of regulatory networks. For networks controlling cell fate decisions, cell fates are associated with model attractors (stable states or cyclic attractors) whose identification and reachability properties are particularly relevant. While synchronous updates assume unlikely instantaneous or identical rates associated with component changes, the consideration of asynchronous updates is more realistic but, for large models, may hinder the analysis of the resulting non-deterministic concurrent dynamics. This complexity hampers the study of asymptotical behaviors, and most existing approaches suffer from efficiency bottlenecks, being generally unable to handle cyclical attractors and quantify attractor reachability. Here, we propose two algorithms providing probability estimates of attractor reachability in asynchronous dynamics. The first algorithm, named Firefront, exhaustively explores the state space from an initial state, and provides quasi-exact evaluations of the reachability probabilities of model attractors. The algorithm progresses in breadth, propagating the probabilities of each encountered state to its successors. Second, Avatar is an adapted Monte Carlo approach, better suited for models with large and intertwined transient and terminal cycles. Avatar iteratively explores the state space by randomly selecting trajectories and by using these random walks to estimate the likelihood of reaching an attractor. Unlike Monte Carlo simulations, Avatar is equipped to avoid getting trapped in transient cycles and to identify cyclic attractors. Firefront and Avatar are validated and compared to related methods, using as test cases logical models of synthetic and biological networks. Both algorithms are implemented as new functionalities of GINsim 3.0, a well-established software tool for logical modeling, providing executable GUI, Java API, and scripting facilities.

Keywords: attractors; discrete asynchronous dynamics; logical modeling; reachability; regulatory network.

Figure 1

Illustration of firefront operation, with $\alpha =\frac{1}{16}$: (1) The exploration starts from initial state v₁ in F associated with probability 1, sets A and N are empty; (2) successors replace v₁ in F, associated with their probabilities; (3–4) states in F are replaced by their successors, but the stable state v₇ goes in A; (4) v₃, v₄, v₆ stay in F with updated probabilities; (5) probability of v₈ in A increases as it is visited again; (6) v₅ goes to N as its probability is lower than α; (7) v₅ is removed from N and put back in F as its probability increased when visited again from v₁. Transitions explored in the current iteration are in blue, their sources being labeled with their probabilities. Red nodes are in A, and gray nodes are in N. The exploration will halt when F is empty or the maximum number of iterations is reached.

Figure 2

Illustration of avatar operation: The transition matrix π is partitioned into the sub-matrices q for transitions between states v₁, …v₄ of the cycle to be discovered (Top Left), and r for transitions leaving the cycle (Top Right). Exploration starts at v₁ (denoted in blue as well as its leaving transitions with their probabilities), v₂ is selected for the second iteration, and v₁ is indicated as being already visited in red. Exploration proceeds until revisiting v₁ at the 5^th step. Having identified a cycle, the rewiring procedure is launched, removing transitions of the cycle (dotted red) and adding transitions toward exits (green). Probabilities are computed, resulting in a new matrix π¹, with $q_{ij}^1=0$ and $r_{ij}^1={({(Id-q)}^{-1}r)}_{ij},i=1,\dots 4$. From v₁, an exit of the cycle is chosen according to these probabilities (step 6).

Figure 3

GUI for the assessment of attractor reachability within ginsim.

Figure 4

Plots computed by firefront and avatar throughout simulations for the random3 (Top) and the sp1 (Bottom) models (see Tables 1, 2). Left plots show the numbers of states to be expanded (in F), of neglected states (in N), and of attractors (in A). Middle plots show the cumulative probabilities of the 3 sets. Right plots show the convergence of the reachability probability of each attractor.

Figure 5

Probabilities of the phenotypes for the bladder tumourigenesis model in the wild type and mutant contexts: probabilities for the double mutant FGRF3 overexpression (FGFR3 E1) and PI3K overexpression (PI3K E1) suggest a slight advantage in mutating FGFR3 in a PI3K-mutated context (by increasing the probability of Proliferation); a third mutation of the tumor suppressor CDKN2A (coding for p16INKa) leads to the sole phenotype Proliferation (see Remy et al., 2015).