Theoretical analysis of inducer and operator binding for cyclic-AMP receptor protein mutants
- PMID: 30256816
- PMCID: PMC6157895
- DOI: 10.1371/journal.pone.0204275
Theoretical analysis of inducer and operator binding for cyclic-AMP receptor protein mutants
Erratum in
-
Correction: Theoretical analysis of inducer and operator binding for cyclic-AMP receptor protein mutants.PLoS One. 2019 Aug 13;14(8):e0221295. doi: 10.1371/journal.pone.0221295. eCollection 2019. PLoS One. 2019. PMID: 31408498 Free PMC article.
Abstract
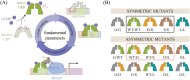
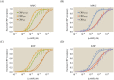
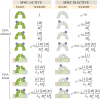
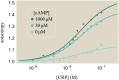
Allosteric transcription factors undergo binding events at inducer binding sites as well as at distinct DNA binding domains, and it is difficult to disentangle the structural and functional consequences of these two classes of interactions. We compare the ability of two statistical mechanical models-the Monod-Wyman-Changeux (MWC) and the Koshland-Némethy-Filmer (KNF) models of protein conformational change-to characterize the multi-step activation mechanism of the broadly acting cyclic-AMP receptor protein (CRP). We first consider the allosteric transition resulting from cyclic-AMP binding to CRP, then analyze how CRP binds to its operator, and finally investigate the ability of CRP to activate gene expression. We use these models to examine a beautiful recent experiment that created a single-chain version of the CRP homodimer, creating six mutants using all possible combinations of the wild type, D53H, and S62F subunits. We demonstrate that the MWC model can explain the behavior of all six mutants using a small, self-consistent set of parameters whose complexity scales with the number of subunits, providing a significant benefit over previous models. In comparison, the KNF model not only leads to a poorer characterization of the available data but also fails to generate parameter values in line with the available structural knowledge of CRP. In addition, we discuss how the conceptual framework developed here for CRP enables us to not merely analyze data retrospectively, but has the predictive power to determine how combinations of mutations will interact, how double mutants will behave, and how each construct would regulate gene expression.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


References
-
- Gama-Castro S, Salgado H, Santos-Zavaleta A, Ledezma-Tejeida D, Muñiz-Rascado L, García-Sotelo JS, et al. RegulonDB Version 9.0: High-level Integration of Gene Regulation, Coexpression, Motif Clustering and Beyond. Nucleic Acids Research. 2016;44(D1):D133–D143. 10.1093/nar/gkv1156 - DOI - PMC - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

