Microtubule Dynamics, Kinesin-1 Sliding, and Dynein Action Drive Growth of Cell Processes

Abstract

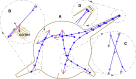
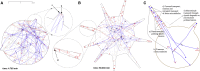
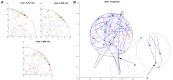
Recent experimental studies of the role of microtubule sliding in neurite outgrowth suggested a qualitative model, according to which kinesin-1 motors push the minus-end-out microtubules against the cell membrane and generate the early cell processes. At the later stage, dynein takes over the sliding, expels the minus-end-out microtubules from the neurites, and pulls in the plus-end-out microtubules that continue to elongate the nascent axon. This model leaves unanswered a number of questions: why is dynein unable to generate the processes alone, whereas kinesin-1 can? What is the role of microtubule dynamics in process initiation and growth? Can the model correctly predict the rates of process growth in control and dynein-inhibited cases? What triggers the transition from kinesin-driven to dynein-driven sliding? To answer these questions, we combine computational modeling of a network of elastic dynamic microtubules and kinesin-1 and dynein motors with measurements of the process growth kinetics and pharmacological perturbations in Drosophila S2 cells. The results verify quantitatively the qualitative model of the microtubule polarity sorting and suggest that dynein-powered elongation is effective only when the processes are longer than a threshold length, which explains why kinesin-1 alone, but not dynein, is sufficient for the process growth. Furthermore, we show that the mechanism of process elongation depends critically on microtubule dynamic instability. Both modeling and experimental measurements show, surprisingly, that dynein inhibition accelerates the process extension. We discuss implications of the model for the general problems of cell polarization, cytoskeletal polarity emergence, and cell process protrusion.

Figure 1

Overview of the model elements. (A) MTs within the discoid cell body, some of which protrude into three processes, are shown in blue as chains of segments between the nodes. Large arrows show the plus ends. (B) Cortex-anchored dynein (red) moves toward the MT minus end (red arrow), which causes MT transport in the direction of its plus end (gray arrows). (C) Kinesin (black) is attached to a pair of intersecting MTs; one MT connects to the cargo domain of the motor and is moved toward the plus end of another MT. The MT to which kinesin connects with its motor domain is shifted toward its minus end. This causes relative sliding of MTs (gray arrows). Note that in the model, kinesin action is distributed to two pairs of nodes at the ends of two overlapping MT segments and that the magnitudes of the opposing forces on two MTs are equal. (D) Process elongation in response to MT pushing against the tip of the processes is shown. To see this figure in color, go online.

Figure 2

Simulation of the process initiation in control cells. (A) MTs are dark blue if slid by kinesin, red if slid by dynein, and otherwise gray. Kinesins are represented as black rods, and dyneins as red, cortex-anchored rods. MT minus ends are thick dots. Polymerizing MT plus ends are red arrows; nonpolymerizing ends are not marked. The inset shows that process formation is driven by kinesins sliding MTs. Most MTs are pushed against the leading edge of the process with their minus ends forward (a), but some are pushed with their plus ends forward (b). (B) Simulation of the process elongation in control cells is shown. Dynein pushes MTs against the tip of the process with their plus ends forward (arrow a). Note that MTs are shown in red if currently pushed by dynein and in dark blue if currently pushed by kinesin. (C) For geometric reasons, dynein can only be effective in long processes in which several dynein motors cooperate to overcome pushing by cytoplasmic kinesin (a). Note that MTs would accumulate at the process’s tip through dynein forward transport unless they are redistributed by random turnover (b) or turned around by random forces and transported back into the cell body by dynein (c). Polymerization of MT plus ends into processes increases the polarity sorting effect of dynein (d). To see this figure in color, go online.

Figure 3

Simulations of motor-perturbed cells. (A) Simulations of cells after kinesin inhibition are shown. Cortex-bound dynein motors push MTs tangentially along the cortex and therefore do not initiate processes. One MT that is being slid by dynein along the cell boundary in this simulation is shown in green. One MT starts to interact with a dynein motor at the later time and is shown in red. (B) Process elongation driven by kinesins (black bars) in dynein-inhibited cells is shown. Kinesin motors, such as the one shown in (b), push against the process tips through MT minus ends (filled circles at the MT ends in the inset marked in (a)). MTs being pushed by kinesin are shown in blue. In both (A) and (B), MTs not interacting with the motors are shown in gray; growing MT plus ends are indicated by the red arrows. To see this figure in color, go online.

Figure 4

Dynamic changes of the process length and MT polarity. (A) Length of simulated processes versus number of MT ends at the process tips is shown. We average the number of MT plus and minus ends located within a narrow 1 μm stripe at the tip of a process during 1 min time intervals and compare the simulation of a control cell (upper row) to the simulated dynein-inhibited cell (lower row). (i and iv) For a single simulated process (control and dynein-inhibited, respectively), these diagrams show process length (green), minus-end numbers at the tip (red bars), and plus-end numbers at the tip (blue bars) as functions of time. (ii and iii) Boxplots show distributions of minus-end (ii) and plus-end (iii) numbers at the process tips of the simulated control cell as functions of the process length. (v and vi) Distributions of minus- (v) and plus-end (vi) numbers at the process tips of the simulated dynein-inhibited cell are shown. (B) Distribution of the MT minus ends and of polymerizing plus ends in the processes longer than 6 μm is shown. We show statistics extracted from single simulation snapshots at intervals of 5 s from two 50-min-long simulations (of control and dynein-inhibited cells, respectively), with nine processes each. The positions are normalized to the interval between 0 (base) and 1 (tip). The vertical axes in histograms show the number of the minus-ends. (i) Histogram of relative minus-end positions in control show monotonic decrease toward the process tip, with relatively few minus ends at the tip. (ii) In the absence of dynein, minus ends are uniformly distributed along processes with a peak at the process tip. (iii) Percentage of retrograde plus-end-trajectories in control (1) and dynein-inhibited (2) cells is shown. Circles show the fraction of the retrograde plus ends in single processes; boxplots visualize their distributions. Mean fractions in control and dynein-inhibited cells are significantly different, with p-value p = 0.0086. (C) The upper row shows experimentally measured growth of the processes’ length (length versus time; time is measured for each individual process starting from the process initiation; see also Fig. S2). The lower row shows simulated process growth: (i and v) control; (ii and vi) dynein-inhibited; (iii and vii) control with taxol; (iv and viii) dynein-inhibited with taxol. To see this figure in color, go online.