A Rationale for Mesoscopic Domain Formation in Biomembranes
- PMID: 30274275
- PMCID: PMC6316292
- DOI: 10.3390/biom8040104
A Rationale for Mesoscopic Domain Formation in Biomembranes
Abstract
Cell plasma membranes display a dramatically rich structural complexity characterized by functional sub-wavelength domains with specific lipid and protein composition. Under favorable experimental conditions, patterned morphologies can also be observed in vitro on model systems such as supported membranes or lipid vesicles. Lipid mixtures separating in liquid-ordered and liquid-disordered phases below a demixing temperature play a pivotal role in this context. Protein-protein and protein-lipid interactions also contribute to membrane shaping by promoting small domains or clusters. Such phase separations displaying characteristic length-scales falling in-between the nanoscopic, molecular scale on the one hand and the macroscopic scale on the other hand, are named mesophases in soft condensed matter physics. In this review, we propose a classification of the diverse mechanisms leading to mesophase separation in biomembranes. We distinguish between mechanisms relying upon equilibrium thermodynamics and those involving out-of-equilibrium mechanisms, notably active membrane recycling. In equilibrium, we especially focus on the many mechanisms that dwell on an up-down symmetry breaking between the upper and lower bilayer leaflets. Symmetry breaking is an ubiquitous mechanism in condensed matter physics at the heart of several important phenomena. In the present case, it can be either spontaneous (domain buckling) or explicit, i.e., due to an external cause (global or local vesicle bending properties). Whenever possible, theoretical predictions and simulation results are confronted to experiments on model systems or living cells, which enables us to identify the most realistic mechanisms from a biological perspective.
Keywords: clusters; domains; lipid rafts; lipids; membranes; mesophase separation; proteins; vesicles.
Conflict of interest statement
The authors declare no conflict of interest.
Figures






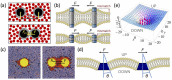

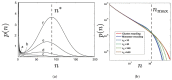
Similar articles
-
Order of lipid phases in model and plasma membranes.Proc Natl Acad Sci U S A. 2009 Sep 29;106(39):16645-50. doi: 10.1073/pnas.0908987106. Epub 2009 Sep 15. Proc Natl Acad Sci U S A. 2009. PMID: 19805351 Free PMC article.
-
Membrane transporter dimerization driven by differential lipid solvation energetics of dissociated and associated states.Elife. 2021 Apr 7;10:e63288. doi: 10.7554/eLife.63288. Elife. 2021. PMID: 33825681 Free PMC article.
-
Molecular view of phase coexistence in lipid monolayers.J Am Chem Soc. 2012 Oct 24;134(42):17543-53. doi: 10.1021/ja304792p. Epub 2012 Oct 12. J Am Chem Soc. 2012. PMID: 23005893
-
Micromechanics of Biomembranes.J Membr Biol. 2022 Dec;255(6):637-649. doi: 10.1007/s00232-022-00254-w. Epub 2022 Jul 14. J Membr Biol. 2022. PMID: 35835874 Review.
-
An outlook on organization of lipids in membranes: searching for a realistic connection with the organization of biological membranes.Prog Lipid Res. 2010 Oct;49(4):378-89. doi: 10.1016/j.plipres.2010.05.001. Epub 2010 May 15. Prog Lipid Res. 2010. PMID: 20478336 Review.
Cited by
-
Interplay of receptor-ligand binding and lipid domain formation during cell adhesion.Front Mol Biosci. 2022 Sep 20;9:1019477. doi: 10.3389/fmolb.2022.1019477. eCollection 2022. Front Mol Biosci. 2022. PMID: 36203878 Free PMC article. Review.
-
LFA-1 nanoclusters integrate TCR stimulation strength to tune T-cell cytotoxic activity.Nat Commun. 2024 Jan 9;15(1):407. doi: 10.1038/s41467-024-44688-3. Nat Commun. 2024. PMID: 38195629 Free PMC article.
-
Structure and Dynamics of GPCRs in Lipid Membranes: Physical Principles and Experimental Approaches.Molecules. 2020 Oct 15;25(20):4729. doi: 10.3390/molecules25204729. Molecules. 2020. PMID: 33076366 Free PMC article. Review.
-
Role of the membrane anchor in the regulation of Lck activity.J Biol Chem. 2022 Dec;298(12):102663. doi: 10.1016/j.jbc.2022.102663. Epub 2022 Nov 11. J Biol Chem. 2022. PMID: 36372231 Free PMC article.
-
Protein overexpression can induce the elongation of cell membrane nanodomains.Biophys J. 2023 Jun 6;122(11):2112-2124. doi: 10.1016/j.bpj.2022.12.009. Epub 2022 Dec 7. Biophys J. 2023. PMID: 36482718 Free PMC article.
References
-
- Alberts B., Johnson A., Lewis J., Ra M., Roberts K., Walter P. Molecular Biology of the Cell. 4th ed. Garland Science; New York, NY, USA: 2002.
-
- Phillips R., Kondev J., Thierot J., Orme N. Physical Biology of the Cell. Garland Science; New York, NY, USA: 2009.
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

