Functional tractography of white matter by high angular resolution functional-correlation imaging (HARFI)

Abstract

Purpose: Functional magnetic resonance imaging with BOLD contrast is widely used for detecting brain activity in the cortex. Recently, several studies have described anisotropic correlations of resting-state BOLD signals between voxels in white matter (WM). These local WM correlations have been modeled as functional-correlation tensors, are largely consistent with underlying WM fiber orientations derived from diffusion MRI, and appear to change during functional activity. However, functional-correlation tensors have several limitations. The use of only nearest-neighbor voxels makes functional-correlation tensors sensitive to noise. Furthermore, adjacent voxels tend to have higher correlations than diagonal voxels, resulting in orientation-related biases. Finally, the tensor model restricts functional correlations to an ellipsoidal bipolar-symmetric shape, and precludes the ability to detect complex functional orientation distributions (FODs).

Methods: We introduce high-angular-resolution functional-correlation imaging (HARFI) to address these limitations. In the same way that high-angular-resolution diffusion imaging (HARDI) techniques provide more information than diffusion tensors, we show that the HARFI model is capable of characterizing complex FODs expected to be present in WM.

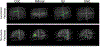
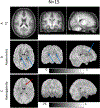
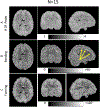
Results: We demonstrate that the unique radial and angular sampling strategy eliminates orientation biases present in tensor models. We further show that HARFI FODs are able to reconstruct known WM pathways. Finally, we show that HARFI allows asymmetric "bending" and "fanning" distributions, and propose asymmetric and functional indices which may increase fiber tracking specificity, or highlight boundaries between functional regions.

Conclusions: The results suggest the HARFI model could be a robust, new way to evaluate anisotropic BOLD signal changes in WM.

Keywords: functional connectivity; functional magnetic resonance imaging; functional pathways; high angular resolution.

Figure 1.

2D example of HARFI fitting. For traditional FCT fit, only neighborhood voxels (8 in 2D, 26 in 3D) are used to fit a tensor (A), from which the major eigenvector is extracted (B). In HARFI fitting, a large number of directions are evaluated (C), and the BOLD signal is integrated over a larger distance for correlation calculation (D), resulting in the HARFI signal defined over a sphere (E).

Figure 2.

Nearest Neighbor bias is removed using the HARFI fitting method. Correlation coefficients for all nearest-neighbor voxels are shown for adjacent voxels (light gray, distance = 1), cube side-diagonal voxels (medium gray, distance = √2), and cube corner-diagonal voxels (dark gray, distance = √3) for all voxels in the WM. Correlation coefficients are always higher for adjacent voxels, causing an orientation bias in three orthogonal directions when fitting spherical harmonic coefficients directly to nearest neighbors (C). The HARFI fit shows no apparent bias in the orientation distributions.

Figure 3.

HARFI is capable of characterizing complex functional orientation distributions. HARFI fits are shown for an axial (A) and coronal (B) slice, with magnified views of crossing or complex distributions. Note that glyphs are shown min-max normalized (as is common in diffusion visualization) in order to highlight orientation contrast. For comparison, functional correlation tensor glyphs are shown, which are restricted to ellipsoidal distributions. Arrows highlight regions of complex orientation distributions.

Figure 4.

HARFI is able to reconstruct functional pathways (top) that are qualitatively similar to known structural pathways (bottom). Visualizations from left to right include the cingulate gyrus (CGC), forceps minor (FMinor), inferior longitudinal fasciculus (ILF), and the uncinate fasciculus (UNC). Structural pathways are created using DTI fiber tractography on the same subject from diffusion data acquired in the same scan session.

Figure 5.

HARFI is able to capture complex, asymmetric functional distributions. Fiber fanning (A, B; red arrows), three-way crossings (C; blue arrows), and bending (D; black arrows) voxels are reconstructed in regions expected to contain complex distributions.

Figure 6.

Individual HARFI indices. Tri-planar views are shown for an individual subject for T1 anatomical image, asymmetric index, and homogeneity index.

Figure 7.

Individual HARFI indices. Tri-planar views are shown for an individual subject for number of peaks, bending index, and fanning index.

Figure 8.

Subject averaged HARFI indices. Tri-planar views are shown averaged over all subjects (N=15) for T1 anatomical image, asymmetric index, and homogeneity index.

Figure 9.

Subject averaged HARFI indices. Tri-planar views are shown averaged over all subjects (N=15) for number of peaks, bending index, and fanning index.

Figure A1.

Bending and Fanning Illustrations. (A) 2D Illustration of functional bending. Two peaks show an angular bend of β degrees. (B) 2D Illustration of functional fanning. Because the angular opening of peak #1 (red, δ₁) is slightly larger than that of peak #2 (blue, δ₂), the functional correlations “spread” from peak #2 to #1, or “converge” as we travel from #1 to #2.