A Kirchhoff-Nernst-Planck framework for modeling large scale extracellular electrodiffusion surrounding morphologically detailed neurons

Abstract

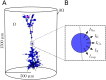
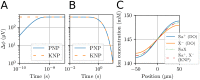
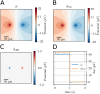
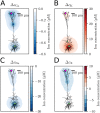
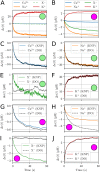
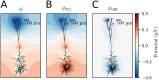
Many pathological conditions, such as seizures, stroke, and spreading depression, are associated with substantial changes in ion concentrations in the extracellular space (ECS) of the brain. An understanding of the mechanisms that govern ECS concentration dynamics may be a prerequisite for understanding such pathologies. To estimate the transport of ions due to electrodiffusive effects, one must keep track of both the ion concentrations and the electric potential simultaneously in the relevant regions of the brain. Although this is currently unfeasible experimentally, it is in principle achievable with computational models based on biophysical principles and constraints. Previous computational models of extracellular ion-concentration dynamics have required extensive computing power, and therefore have been limited to either phenomena on very small spatiotemporal scales (micrometers and milliseconds), or simplified and idealized 1-dimensional (1-D) transport processes on a larger scale. Here, we present the 3-D Kirchhoff-Nernst-Planck (KNP) framework, tailored to explore electrodiffusive effects on large spatiotemporal scales. By assuming electroneutrality, the KNP-framework circumvents charge-relaxation processes on the spatiotemporal scales of nanometers and nanoseconds, and makes it feasible to run simulations on the spatiotemporal scales of millimeters and seconds on a standard desktop computer. In the present work, we use the 3-D KNP framework to simulate the dynamics of ion concentrations and the electrical potential surrounding a morphologically detailed pyramidal cell. In addition to elucidating the single neuron contribution to electrodiffusive effects in the ECS, the simulation demonstrates the efficiency of the 3-D KNP framework. We envision that future applications of the framework to more complex and biologically realistic systems will be useful in exploring pathological conditions associated with large concentration variations in the ECS.

Fig 1. Model system of a 3-D cylinder of ECS containing a morphologically detailed neuron.

(A) The simulated domain is denoted by Ω, and the boundary is denoted by ∂Ω. Exchange of ions between the neuron and ECS was modeled as a set of point sources (marked by blue dots). Two measurement points were used to create time series in the Results-section. These are shown as the green and purple points. (B) Each point source was included as a sink/source of each ion species, as well as a capacitive current.

Fig 2. Electrodiffusion in a simple 1-D system containing no current sources.

The system had an initial step concentration of NaX being 140 mM for x < 0 and 150 mM for x > 0. (A) Dynamics of the potential difference between the left and right sides of the system on a short timescale. Δϕ is defined as Δϕ = ϕ(x_right) − ϕ(x_left), where x_right = 0.1 μm and x_left = −0.1 μm. In PNP simulations, the system spent about 10 ns building up the potential difference across the system. In KNP simulations, the steady-state potential was assumed to occur immediately. After 10 ns, the schemes were virtually indistinguishable. (B) Dynamics of the potential between x_right = 50 μm and x_left = −50 μm on a long timescale. The PNP- and KNP-schemes gave identical predictions. (C) The concentration profiles in the system at t = 1.0 s as obtained with KNP, DO and according to the theoretical approximation when NaX develops as a single concentration moving by diffusion with a modified diffusion coefficient.

Fig 3. Application with a K⁺ point source/sink pair in a 3-D box containing a standard ECS ion solution.

The source and sink were turned on at t = 0 s, and turned off at t = 1 s. The simulation was stopped at t = 2 s. (A) The total electrical potential ϕ at the end of the stimulus period (t = 1.0 s) in a plane intersecting the source and sink. (B) The volume conductor component of the electrical potential, ϕ_VC. (C) The diffusive component of the electrical potential ϕ_diff. (D) The difference in the electric potential between points close to the point sources (blue line), also shown is the differences in the VC component of the potential (stapled yellow line). Δϕ is defined as Δϕ = ϕ(x_left) − ϕ(x_right), where x_left and x_right were points 5 μm away from the left and right, respectively (see Methods).

Fig 4. (A)-(D)The change in ionic concentration for Ca²⁺, K⁺, Na⁺, and X⁻, respectively, as measured at t = 80 s, compared to the initial concentration.

Δc_k is the change in concentration from the initial value, defined as Δc_k = c_k(t) − c_k(0). The concentrations were measured in a 2-D slice going through the center of the computational mesh, and the neuron morphology was stenciled in. The green and purple dots signify selected measurement points in the ECS near the soma (green) and apical dendrites (purple) of the neuron, which are reference points for the analysis in the following sections.

Fig 5. Ion concentration dynamics at selected measurement points.

The locations of the measurement points were in the ECS near the soma (green) and apical dendrites (purple) of the neuron. Δc(t) is the change in concentration from the initial value, defined as Δc(t) = c(t) − c(0). (A)-(B) Dynamics of all ion species as predicted by the KNP-scheme. (C)-(F) A comparison between the KNP and DO predictions at the measurement point near the soma. (G)-(J) A comparison between the KNP and DO predictions at the measurement point near the apical dendrites. (C)-(J) To generate the DO predictions, we set the ECS field to zero, which ensured that the ECS dynamics was due to diffusion only.

Fig 6. Spatial profile of the ECS potential at a selected time point.

The ECS potential was averaged over a 100 ms interval between t = 79.9 s and 80 s. This averaging low-pass filters the potential. (A) ECS potential as predicted by the KNP-scheme. (B) The VC component of the potential. (C) The diffusive component of the potential.

Fig 7. Dynamics of the ECS potential at selected measurement points.

The selected measurement points were in the ECS near the soma (green) and apical dendrites (purple) of the neuron. (A)-(B) Dynamics of the ECS potential for the first 80 s of the simulation. Each data point represent an average over a 100 ms time interval, which effectively low-pass filtered the signal. (C)-(D) High resolution time series for the ECS potential during a neural AP. The data were not low-pass filtered, but had a temporal resolution of 0.1 ms.