Interactive reservoir computing for chunking information streams

Abstract

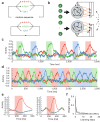
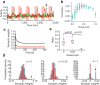
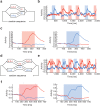
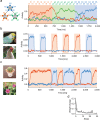
Chunking is the process by which frequently repeated segments of temporal inputs are concatenated into single units that are easy to process. Such a process is fundamental to time-series analysis in biological and artificial information processing systems. The brain efficiently acquires chunks from various information streams in an unsupervised manner; however, the underlying mechanisms of this process remain elusive. A widely-adopted statistical method for chunking consists of predicting frequently repeated contiguous elements in an input sequence based on unequal transition probabilities over sequence elements. However, recent experimental findings suggest that the brain is unlikely to adopt this method, as human subjects can chunk sequences with uniform transition probabilities. In this study, we propose a novel conceptual framework to overcome this limitation. In this process, neural networks learn to predict dynamical response patterns to sequence input rather than to directly learn transition patterns. Using a mutually supervising pair of reservoir computing modules, we demonstrate how this mechanism works in chunking sequences of letters or visual images with variable regularity and complexity. In addition, we demonstrate that background noise plays a crucial role in correctly learning chunks in this model. In particular, the model can successfully chunk sequences that conventional statistical approaches fail to chunk due to uniform transition probabilities. In addition, the neural responses of the model exhibit an interesting similarity to those of the basal ganglia observed after motor habit formation.

Fig 1. Learning of a single chunk repeated in random sequence.

(a) Input sequence repeating a single chunk. In this example, the chunk is composed of four alphabets (a, b, c, d). The components and lengths of random sequences varied during the repetition of chunks. (b) Example responses are shown for input neurons. (c) In the dual RC model, two non-identical reservoirs are activated by the same set of input neurons. Readout weights of each RC system undergo supervised learning with a teaching signal given by the output of the partner network. (d) and (e) Pre- and post-learning trial averaged activities of a readout unit are shown, respectively. Shaded intervals designate the presentation periods of the chunk. The other readout unit exhibited a similar activity pattern. (f) Readout activity was trained with many-to-one input projections. The fraction of input neurons projecting to a reservoir neuron was 10% (red), 40% (green) and 70% (black).

Fig 2. Readout activity after learning detects multiple chunks.

(a) Top, Three chunks a-b-c-d (red), e-f-g-h (green), and i-j-k-l (blue) separated by random sequences are recurred at equal frequencies in input. Bottom, The three chunks are repeated without the intervals of random sequences. (b) Each reservoir was connected to three readout units. (c) Selective readout responses to the individual chunks (colored intervals) were self-organized. Input contained random sequences. The responses are colored according to their selectivity to the chunks. (d) The same chunks were repeated without breaks by random sequences. Previous models of chunking typically processed such input sequences. (e) Readout activities formed with (left) and without (right) random sequence intervals were averaged over the recurrence of chunk “a-b-c-d”. (f) Time evolution of average readout weights is shown at every step of learning with (gray) and without (black) random sequence intervals.

Fig 3. Principal component analysis of recurrent networks.

Each recurrent network consists of 300 neurons. (a) Left, Activities of two reservoir networks are projected onto the top five eigenvectors of the correlation matrix. Shaded areas indicate the intervals of the presentation of chunks. Numerals on the right side show the variances explained. Right, The low-dimensional trajectories of the two reservoir modules are shown in the space spanned by PC1 to PC3. Red/blue or magenta/cyan portions show trajectories during the epoch of non-vanishing or vanishing teacher signals, respectively. (b) The eigenvalues of PCs are shown in a logarithmic scale. (c) The correlation coefficient between each PC and the readout activity is shown. (d) The length of readout weights projected onto each eigenvector is shown for first 100 eigenstates. (e) “Within-self” difference between the R1-output and the projected R1-output (green) and “between-partner” difference between the R2-output and the projected R1-output (blue) are shown for all the eigenstates before (dashed) and after (solid) learning. Insets display magnified versions for major eigenstates.

Fig 4. Effects of noise on successful chunk learning.

(a) Activity of a readout unit after learning a chunk at different noise levels: σ = 0 (black), 0.25 (red) and 1 (green). Without noise, the readout unit still learned to respond to a portion of input, but this portion did not necessarily belong to a chunk (vertical arrow). (b) Learning performance is a non-monotonic function of the noise level. The optimal performance was obtained at σ = 0.4–0.6 when the scaling factor in Equation 4 was set as g_G = 1.5 (cyan). The effect of noise on the learning performance was not significantly changed when the scaling factor was simultaneously reduced with the noise level (gray). (c) Evolution of the norm of readout weights during learning is shown for σ = 0 (black), 0.25 (red) and 1 (green). (d) The distributions of readout weights from chunk-encoding (red) and non-encoding (blue) reservoir neurons are shown after learning at different noise levels. Arrows indicate the maximum weight values from the chunk-encoding neurons. (e) The fraction of strong readout weights (see the main text) from the encoding neurons is shown for different noise levels. The fraction is significantly larger for σ = 0.25 compared with σ = 0 and 1 (p<0.01, Mann–Whitney U test).

Fig 5. Learning chunks with mutual overlaps.

(a) Two chunks shared the last component “d” in a random input sequence. (b) Activities of two readout units were selective to different chunks after learning. (c) The average response profiles are shown for the two readout units. (d) Two chunks shared the middle components “d-e” in a random input sequence. (e) and (f), Activities of two readout units and the average response profiles are shown, respectively.

Fig 6. Chunking complex temporal inputs.

(a) Sequence inputs were generated by a graph with uniform transition probabilities and community structure. The graph was modified from [23]. (b) Sequence of high -resolution (97x97x3) visual stimuli, where the factor 3 represents the three RGB channels, was chunked. White intervals show periods of Gaussian noise. (c) Sequence of high-resolution (97x97x3) visual stimuli was chunked. (d) Learning curves are compared for the images shown in (c) between high (black) and low (gray) resolution versions. The images were repeatedly presented without noise intervals.