Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2018 Oct 9;11(10):1919.
doi: 10.3390/ma11101919.

Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study

Yanchao Wang  1 , ZhengMing Huang  2
Affiliations
Review

Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study

Yanchao Wang et al. Materials (Basel). .

Abstract

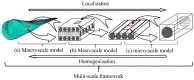
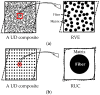
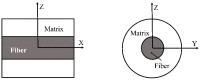
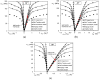
Elasto-plastic models for composites can be classified into three categories in terms of a length scale, i.e., macro scale, meso scale, and micro scale (micromechanics) models. In general, a so-called multi-scale model is a combination of those at various length scales with a micromechanics one as the foundation. In this paper, a critical review is made for the elastoplastic models at the micro scale, and a comparative study is carried out on most popular analytical micromechanics models for the elastoplastic behavior of long fibrous composites subjected to a static load, meaning that creep and dynamic response are not concerned. Each model has been developed essentially following three steps, i.e., an elastic homogenization, a rule to define the yielding of a constituent phase, and a linearization for the elastoplastic response. The comparison is made for all of the three aspects. Effects of other issues, such as the stress field fluctuation induced by a high contrast heterogeneity, the stress concentration factors in the matrix, and the different approaches to a plastic Eshelby tensor, are addressed as well. Correlation of the predictions by different models with available experimental data is shown.

Keywords: analytical models; elastoplastic behavior; fibrous composites; micromechanics.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Figures

Figure 1
Figure 1
Schematic of a multi-scale framework: (a) macro-scale model; (b) meso-scale model; (c) micro-scale model.
Figure 2
Figure 2
Schematic of a representative volume element RVE and a repeating unit cell (RUC) (solid line-undeformed, dash line-deformed). (a) An RVE for a unidirectional (UD) composite with randomly distributed fibers; (b) an RUC for a UD composite with periodically distributed fibers.
Figure 3
Figure 3
Establishment of elastoplastic models for composites.
Figure 4
Figure 4
Imperfect interface phenomenon in fibrous composites. (a) Crack growth in a SiC/SiC woven composite under cyclic load [242]; (b) Ear-hole formation in a SiC/Ti-6Al-4V composite [243]; (c) Interphase produced by chemical reaction in a SiC/Ti-6Al-4V composite [244]; (d) BN coated T300 fiber [245].
Figure 5
Figure 5
Schematic of an RUC for a UD composite.
Figure 6
Figure 6
Schematic of a multi-fiber model and a single fiber model. (a) Multi-fiber model; (b) single fiber model.
Figure 7
Figure 7
Schematic for generalized self-consistent method (GSCM).
Figure 8
Figure 8
Illustration of a typical elastoplastic stress-strain curve.
Figure 9
Figure 9
Comparison between elastoplastic models (IM7/8551-7 UD composite). (a) Transverse compression; (b) In-plane shear.
Figure 10
Figure 10
Comparison between elastoplastic models (E-Glass/Epoxy UD composite). (a) Transverse compression; (b) In-plane shear.
Figure 11
Figure 11
Comparison between elastoplastic models (AS4/Peek UD composite). (a) 30° off-axis tension; (b) 45° off-axis tension; (c) 60° off-axis tension.
Figure 12
Figure 12
Short fiber reinforced polyamide composite under uniaxial tension [280]. (a) Longitudinal tension; (b) Transverse tension.
Figure 13
Figure 13
Finite element analysis (FEA) strain contour for short fiber reinforced polyamide composite [280].
Figure 14
Figure 14
Comparison between the first and second-moment approach. (a) Ceramic reinforced aluminum composite (aspect ratio = 1, plastic parameter n = 0.05); (b) Ceramic reinforced aluminum composite (aspect ratio = 3, plastic parameter n = 0.05); (c) Ceramic reinforced aluminum composite (aspect ratio = 3, plastic parameter n = 0.4); (d) two-phase steel with martensite inclusions (aspect ratio = 3, plastic parameter n = 0.31).
Figure 15
Figure 15
Comparison of models with/without stress concentration factors (SCFs)—IM7/8551-7 UD composite. (a) Transverse compression; (b) In-plane shear.
Figure 16
Figure 16
Comparison of models with/without stress concentration factors (SCFs)—E-glass/Epoxy UD composite. (a) Transverse compression; (b) In-plane shear.
Figure 17
Figure 17
Comparison of models with/without SCFs—AS4/Peek UD composite. (a) 30° Off-axis tension; (b) 45° Off-axis tension; (c) 60° Off-axis tension.
Figure 17
Figure 17
Comparison of models with/without SCFs—AS4/Peek UD composite. (a) 30° Off-axis tension; (b) 45° Off-axis tension; (c) 60° Off-axis tension.
Figure 18
Figure 18
Schematic of linearization theories.
Figure 19
Figure 19
Schematic of the incremental-secant linearization [112].
Figure 20
Figure 20
Comparison among linearizations–IM7/8551-7 UD composite. (a) Transverse compression; (b) In-plane shear.
Figure 21
Figure 21
Comparison among linearizations–E-Glass/Epoxy UD composite. (a) Transverse compression; (b) In plane shear.
Figure 22
Figure 22
Comparison among linearizations–AS4/Peek UD composite. (a) 30° off-axis tension; (b) 45° off-axis tension; (c) 60° off-axis tension.
Figure 23
Figure 23
Comparison among the four approaches to determine an Eshelby tensor. (a) Longitudinal tension—(IM7/8551-7 UD composites); (b) Transverse compression—(IM7/8551-7 UD composites); (c) In-plane shear—(IM7/8551-7 UD composites); (d) 30° off-axis tension—(AS4/Peek UD composite); (e) 45° off-axis tension—(AS4/Peek UD composite); (f) 60° off-axis tension—(AS4/Peek UD composite).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Dvorak G.J., Bahei-El-Din Y. Plasticity analysis of fibrous composites. J. Appl. Mech. 1982;49:327–335. doi: 10.1115/1.3162088. - DOI
    1. Camanho P.P., Matthews F.L. Stress analysis and strength prediction of mechanically fastened joints in FRP: A review. Compos. Part A Appl. Sci. Manuf. 1997;28:529–547. doi: 10.1016/S1359-835X(97)00004-3. - DOI
    1. Liu P.F., Zheng J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010;31:3825–3834. doi: 10.1016/j.matdes.2010.03.031. - DOI
    1. Chandra R., Singh S.P., Gupta K. Damping studies in fiber-reinforced composites—A review. Compos. Struct. 1999;46:41–51. doi: 10.1016/S0263-8223(99)00041-0. - DOI
    1. Daniel I.M., Ishai O., Daniel I.M., Daniel I. Engineering Mechanics of Composite Materials. Volume 3 Oxford University Press; New York, NY, USA: 1994.

LinkOut - more resources