A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials

Abstract

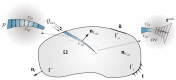
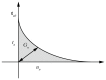
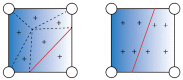
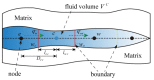
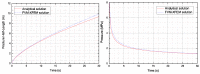
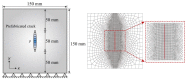
High-pressure hydraulic fractures are often reported in real engineering applications, which occur due to the existence of discontinuities such as cracks, faults, or shear bands. In this paper, a hybrid finite volume and extended finite element method (FVM-XFEM) is developed for simulating hydro-fracture propagation in quasi-brittle materials, in which the coupling between fluids and deformation is considered. Flow within the fracture is modelled using lubrication theory for a one-dimensional laminar flow that obeys the cubic law. The solid deformation is governed by the linear momentum balance equation under quasi-static conditions. The cohesive crack model is used to analyze the non-linear fracture process zone ahead of the crack tip. The discretization of the pressure field is implemented by employing the FVM, while the discretization of the displacement field is accomplished through the use of the XFEM. The final governing equations of a fully coupled hydro-mechanical problem is solved using the Picard iteration method. Finally, the validity of the proposed method is demonstrated through three examples. Moreover, the fluid pressure distribution along the fracture, the fracture mouth width, and the pattern of the fracture are investigated. It is shown that the numerical results correlated well with the theoretical solutions and experimental results.

Keywords: arbitrary crack propagation; extended finite element method (XFEM); finite volume method (FVM); hydraulic fracturing; quasi-brittle materials.

Figure 1

The definition and boundary conditions of a hydraulic fracturing body within a geomechanical discontinuity.

Figure 2

Cohesive softening law.

Figure 3

The enriched nodal points of a two-dimensional finite element including a discontinuity.

Figure 4

Numerical integration of an enriched element.

Figure 5

Fluid cells within a fracture using the finite volume method.

Figure 6

Flow chart of the finite volume and extended finite element method (FVM-XFEM) method.

Figure 7

A hydraulic-driven fracture propagation in an imperious domain. A schematic representation of the Khristianovic–Geertsma–de Klerk (KGD) problem, the geometry, the boundary conditions, and the finite element mesh.

Figure 8

Comparison of the numerical and analytical solutions regarding: (left) the fracture width at the crack mouth and (right) the fracture width profile.

Figure 9

Comparison of the numerical and analytical solutions regarding: (left) the fracture half-length and (right) the fracture mouth pressure.

Figure 10

Relative error for the fracture width, the fracture half-length, and the fracture mouth pressure using: (left) the FVM-XFEM method and (right) the Carrier et al. [22] model.

Figure 11

A schematic illustration of the hydraulic fracturing (HF) test: (left) Problem definition and (right) the XFEM meshes.

Figure 12

The test process (see a,b) and chart of the fracture propagation path containing both the test results (see c–h) and the numerical results (i).

Figure 13

The contours of the stress distributions using FVM-XFEM (unit: MPa).

Figure 14

Comparison of the numerical and test results regarding: (left) the fracture width and (right) the fluid pressure distribution.

Figure 15

A concrete gravity dam under hydrostatic pressure: the geometry, boundary conditions (left), and XFEM meshes (right).

Figure 16

The crack mouth opening displacement (left) and the water pressure distribution along the crack (right).

Figure 17

The contour of maximum principal stress using the coupling FVM-XFEM method (left) and the patterns of crack growth in the concrete dam using the FVM-XFEM method and the “constant pressure algorithm” (right).