Transitions in synchronization states of model cilia through basal-connection coupling
- PMID: 30305422
- PMCID: PMC6228470
- DOI: 10.1098/rsif.2018.0450
Transitions in synchronization states of model cilia through basal-connection coupling
Abstract
Despite evidence for a hydrodynamic origin of flagellar synchronization between different eukaryotic cells, recent experiments have shown that in single multi-flagellated organisms, coordination hinges instead on direct basal body connections. The mechanism by which these connections lead to coordination, however, is currently not understood. Here, we focus on the model biflagellate Chlamydomonas reinhardtii, and propose a minimal model for the synchronization of its two flagella as a result of both hydrodynamic and direct mechanical coupling. A spectrum of different types of coordination can be selected, depending on small changes in the stiffness of intracellular couplings. These include prolonged in-phase and anti-phase synchronization, as well as a range of multi-stable states induced by spontaneous symmetry breaking of the system. Linking synchrony to intracellular stiffness could lead to the use of flagellar dynamics as a probe for the mechanical state of the cell.
Keywords: Chlamydomonas reinhardtii; cilia; cytoskeleton; flagella; microhydrodynamics; oscillators; synchronization.
© 2018 The Author(s).
Conflict of interest statement
We declare we have no competing interests.
Figures
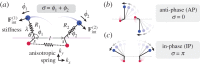

 , for (a)
, for (a)  , (b)
, (b)  and (c)
and (c)  . In each case (starting with
. In each case (starting with  ), IP (blue) and AP (red) synchronized states are obtained for
), IP (blue) and AP (red) synchronized states are obtained for  and
and  , respectively, over a timescale inversely proportional to
, respectively, over a timescale inversely proportional to  . (d) Values of
. (d) Values of  measured from numerical simulations (circles) compare favourably with equation (3.2) for sufficiently soft internal springs. Other model parameters as given in table 1. (Online version in colour.)
measured from numerical simulations (circles) compare favourably with equation (3.2) for sufficiently soft internal springs. Other model parameters as given in table 1. (Online version in colour.)
 . In each simulation
. In each simulation  . Other parameters are shown in table 1. (a–c) Phase sum
. Other parameters are shown in table 1. (a–c) Phase sum  and (d–f) external rotor radii
and (d–f) external rotor radii  are shown as functions of time for various values of ky. (g) The mean value of phase sum
are shown as functions of time for various values of ky. (g) The mean value of phase sum  and (h) external rotor radius
and (h) external rotor radius  are computed from numerical solutions (green) and compared with analytical predictions of equation (4.1) (dashed) and equations (4.2), (4.3) (dotted). (Online version in colour.)
are computed from numerical solutions (green) and compared with analytical predictions of equation (4.1) (dashed) and equations (4.2), (4.3) (dotted). (Online version in colour.)
 ). (a) Steady state
). (a) Steady state  as a function of ky for various ciliary spacings (
as a function of ky for various ciliary spacings ( , 20, 25, 35, 50,
, 20, 25, 35, 50,  ). Numerical solutions (smooth, coloured) are shown alongside analytical predictions to leading order (dashed, black) and second order in
). Numerical solutions (smooth, coloured) are shown alongside analytical predictions to leading order (dashed, black) and second order in  (dashed, coloured). The transition zone boundaries are quantified by
(dashed, coloured). The transition zone boundaries are quantified by  (red crosses) and
(red crosses) and  (blue crosses), respectively. (b) These are shown as a function of l, together with leading order (black) and second order in
(blue crosses), respectively. (b) These are shown as a function of l, together with leading order (black) and second order in  (coloured) analytical predictions. (Online version in colour.)
(coloured) analytical predictions. (Online version in colour.)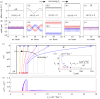
 and (b) external radii
and (b) external radii  and
and  . Results are shown for
. Results are shown for  , 0.006, 0.007, 0.017,
, 0.006, 0.007, 0.017,  with
with  and
and  . For intermediate values of ky, the external rotors display a permanent difference in their average radii despite being identical. Electronic supplementary material movies 1–5 show the dynamics for (i)–(v), respectively. (c) Value of
. For intermediate values of ky, the external rotors display a permanent difference in their average radii despite being identical. Electronic supplementary material movies 1–5 show the dynamics for (i)–(v), respectively. (c) Value of  as a function of ky for various values of l (results shown for
as a function of ky for various values of l (results shown for  , 20, 25, 35, 50,
, 20, 25, 35, 50,  ). The transition zone boundaries are quantified by
). The transition zone boundaries are quantified by  (red crosses) and
(red crosses) and  (blue crosses) respectively; dashed black lines show far-field analytical predictions to leading order (from equation (4.1)). (d) Measured boundaries compared with leading order far-field analytical results. (e) The variance of the time-dependent phase sum,
(blue crosses) respectively; dashed black lines show far-field analytical predictions to leading order (from equation (4.1)). (d) Measured boundaries compared with leading order far-field analytical results. (e) The variance of the time-dependent phase sum,  , for given values of ky and l, reveals large excursions in the phase sum prior to the bifurcation (see (a(ii)) for the raw time-dependent signal). (Online version in colour.)
, for given values of ky and l, reveals large excursions in the phase sum prior to the bifurcation (see (a(ii)) for the raw time-dependent signal). (Online version in colour.)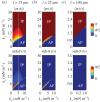
 as functions of kx and ky for external rotor separations (a)
as functions of kx and ky for external rotor separations (a)  , (b)
, (b)  , and (c)
, and (c)  . White dotted lines correspond to the blue bifurcation plot in figure 5c. For small kx, the system is capable of supporting intermediate phase-locked states, with
. White dotted lines correspond to the blue bifurcation plot in figure 5c. For small kx, the system is capable of supporting intermediate phase-locked states, with  . However, for larger kx, an abrupt transition between AP and IP occurs. (Online version in colour.)
. However, for larger kx, an abrupt transition between AP and IP occurs. (Online version in colour.)References
-
- Gray J, Hancock GJ. 1955. The propulsion of sea-urchin spermatozoa. J. Exp. Biol. 32, 802–814.
-
- Knight-Jones EW. 1954. Relations between metachronism and the direction of ciliary beat in metazoa. Q. J. Microsc. Sci. 95, 503–521.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
