Explicit ions/implicit water generalized Born model for nucleic acids

Abstract

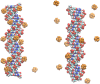
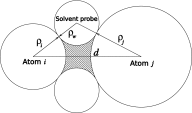
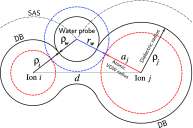
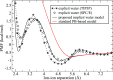
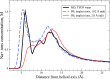
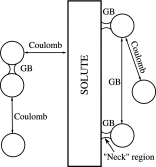
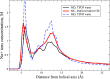
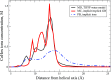
The ion atmosphere around highly charged nucleic acid molecules plays a significant role in their dynamics, structure, and interactions. Here we utilized the implicit solvent framework to develop a model for the explicit treatment of ions interacting with nucleic acid molecules. The proposed explicit ions/implicit water model is based on a significantly modified generalized Born (GB) model and utilizes a non-standard approach to define the solute/solvent dielectric boundary. Specifically, the model includes modifications to the GB interaction terms for the case of multiple interacting solutes-disconnected dielectric boundary around the solute-ion or ion-ion pairs. A fully analytical description of all energy components for charge-charge interactions is provided. The effectiveness of the approach is demonstrated by calculating the potential of mean force for Na⁺-Cl^- ion pair and by carrying out a set of Monte Carlo (MC) simulations of mono- and trivalent ions interacting with DNA and RNA duplexes. The monovalent (Na⁺) and trivalent (CoHex³⁺) counterion distributions predicted by the model are in close quantitative agreement with all-atom explicit water molecular dynamics simulations used as reference. Expressed in the units of energy, the maximum deviations of local ion concentrations from the reference are within k _B T. The proposed explicit ions/implicit water GB model is able to resolve subtle features and differences of CoHex distributions around DNA and RNA duplexes. These features include preferential CoHex binding inside the major groove of the RNA duplex, in contrast to CoHex biding at the "external" surface of the sugar-phosphate backbone of the DNA duplex; these differences in the counterion binding patters were earlier shown to be responsible for the observed drastic differences in condensation propensities between short DNA and RNA duplexes. MC simulations of CoHex ions interacting with the homopolymeric poly(dA·dT) DNA duplex with modified (de-methylated) and native thymine bases are used to explore the physics behind CoHex-thymine interactions. The simulations suggest that the ion desolvation penalty due to proximity to the low dielectric volume of the methyl group can contribute significantly to CoHex-thymine interactions. Compared to the steric repulsion between the ion and the methyl group, the desolvation penalty interaction has a longer range and may be important to consider in the context of methylation effects on DNA condensation.

FIG. 1.

Qualitatively different distributions of multivalent CoHex³⁺ ions around the DNA duplex in the explicit (left) and implicit (right) water. Shown are the representative configurations from an all-atom MD simulation of explicit CoHex ions around a 25 base pair long DNA duplex. Ion distribution resulting from the standard explicit water treatment (TIP3P, left) is compared to the one based on one of the latest GB models available in AMBER (right).

FIG. 2.

Sketch of the dielectric boundary (DB) around a pair of non-bonded solute atoms (ions) in a solvent, separated by a distance d. The DB is defined as a surface around the volume inaccessible to a solvent probe of radius ${\rho }_w$ [Richards-Connolly molecular surface (MS)]. This volume consists of two atomic spheres determined by atomic dielectric radii ρ_i and ρ_j and a region between these spheres (depicted as dashed area) inaccessible to the solvent probe and called the “Neck” region.

FIG. 3.

The geometry of the proposed dielectric boundary (DB) for a pair of ions (atoms) separated by a distance d < a_i + 2$r_w$ + a_j. Ions and water probe van der Waals surfaces, related to the corresponding van der Waals radii a_i, a_j, and $r_w$, are depicted by red and blue dashed lines, respectively. The DB of the ion pair is defined by the effective ionic (atomic) dielectric radii ρ_i and ρ_j, Eq. (12), and by the effective water probe dielectric radius ${\rho }_w$ which is specified by the distance from the SAS to the DB. For the solvent separated configurations (d > a_i + 2$r_w$ + a_j), the ion pair DB consists of two spheres of radii ρ_i and ρ_j.

FIG. 4.

Na⁺–Cl⁻ ion pair PMF W(d) [Eq. (10)] calculated using the GB approach with the analytical estimation of the “Sphere” [Eq. (6)] and “Neck” [Eq. (7)] integrals and the new dielectric boundary (DB) definition (see Fig. 3) (black solid line), numerical solution of PB equation with the “standard” solvent excluded surface (SES) based definition of the DB and water probe radius $r_w$ = 1.4 Å (solid red line), and the results from the MD simulations with explicit TIP3P (stars) and SPC/E (diamonds) water models.

FIG. 5.

Na⁺ ion cylindrical distributions around the 25 bp poly(dA·dT) DNA duplex derived from the explicit water MD simulations with the TIP3P water model (thick solid black line) and from the non-linear PB calculation using experimental Na⁺ value 1.02 Å for monovalent ion radii (dashed blue line) and “standard” 2 Å Na⁺ radius (thin solid red line).

FIG. 6.

Solute-ion and ion-ion interaction modes in the proposed explicit ions/implicit water model. Interactions between ions separated by a layer of the solvent (no ion-ion “Neck” formed) are estimated via the modified GB equations resulting in the Coulomb law behavior. For smaller separations (“Necks” formed), ion-ion interactions are estimated via the canonical GB equation. Interactions between two ions, both forming “Necks” with the solute, are estimated via the canonical GB equation at any ion-ion distance. Interactions between the solute atoms and ions being within ion-solute “Neck” distance are estimated via the canonical GB equation. At larger ion-solute distances, the interactions are estimated via the modified GB equations approximating the Coulomb law behavior. All the interactions within the (singly connected) solute are estimated via the canonical GB.

FIG. 7.

Na⁺ ion cylindrical distributions around the 25 bp poly(dA·dT) DNA duplex derived from the MC simulations using the proposed explicit ions/implicit water GB model (thick solid red line) and from the explicit water MD simulations with the TIP3P water model (solid black line) and with the TIP4-Ew water model (dashed blue line). The GB based result is shown for the optimized “Neck” integrals scaling parameter n_j = 0.4.

FIG. 8.

CoHex ion distributions around the 25 bp homopolymeric poly(dA·dT) DNA duplex derived from the MC simulations using the proposed explicit ions/implicit water GB model (thick solid red line) from the explicit water MD simulations using the TIP3P water model (thin solid black line) and from the non-linear PB calculation with explicit CoHex ions (dot-dashed blue line). The GB derived results are shown for the optimized “Neck” integrals scaling parameter n_j = 0.9.

FIG. 9.

Representative snapshots of CoHex ions (orange) binding to 25 bp DNA and RNA duplexes from explicit (TIP3P) water MD simulations (left) and from the proposed explicit ions/implicit water GB model used in MC simulations (right). CoHex ions bound to the GpC steps in the major grooves of the mixed sequence DNA duplexes are shown in green.