Dipolar exchange quantum logic gate with polar molecules

Abstract

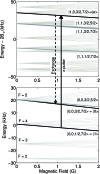
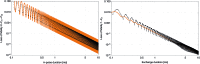
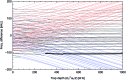
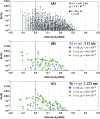
We propose a two-qubit gate based on dipolar exchange interactions between individually addressable ultracold polar molecules in an array of optical dipole traps. Our proposal treats the full Hamiltonian of the ¹Σ⁺ molecule NaCs, utilizing a pair of nuclear spin states as storage qubits. A third rotationally excited state with rotation-hyperfine coupling enables switchable electric dipolar exchange interactions between two molecules to generate an iSWAP gate. All three states are insensitive to external magnetic and electric fields. Impacts on gate fidelity due to coupling to other molecular states, imperfect ground-state cooling, blackbody radiation and vacuum spontaneous emission are small, leading to potential fidelity above 99.99% in a coherent quantum system that can be scaled by purely optical means.

Fig. 1. (A) iSWAP gate based on dipolar exchange between a pair of molecular states with opposite parity. The colored sphere of the |e(A) iSWAP gate based on dipolar exchange between a pair of molecular states with opposite parity. The colored sphere of the |e〉 state represents the wavefunction amplitude of the dipole direction for an state represents the wavefunction amplitude of the dipole direction for an N = 1, m_N = 0 state, where the quantization axis is horizontal. The states |0 = 0 state, where the quantization axis is horizontal. The states |0〉 and |1〉 are hyperfine sublevels of the rotational ground state and |1 = 0 state, where the quantization axis is horizontal. The states |0〉 and |1〉 are hyperfine sublevels of the rotational ground state are hyperfine sublevels of the rotational ground state N = 0. Superpositions of |e = 0. Superpositions of |e〉 and |0〉 or |1〉 produce an electric dipole moment that oscillates at a frequency corresponding to approximately twice the rotational constant of the molecule and couples to a nearby qubit. The four panels in (A) show the initial state |0;1〉 evolving through the gate to and |0 = 0. Superpositions of |e〉 and |0〉 or |1〉 produce an electric dipole moment that oscillates at a frequency corresponding to approximately twice the rotational constant of the molecule and couples to a nearby qubit. The four panels in (A) show the initial state |0;1〉 evolving through the gate to or |1 = 0. Superpositions of |e〉 and |0〉 or |1〉 produce an electric dipole moment that oscillates at a frequency corresponding to approximately twice the rotational constant of the molecule and couples to a nearby qubit. The four panels in (A) show the initial state |0;1〉 evolving through the gate to produce an electric dipole moment that oscillates at a frequency corresponding to approximately twice the rotational constant of the molecule and couples to a nearby qubit. The four panels in (A) show the initial state |0;1 = 0. Superpositions of |e〉 and |0〉 or |1〉 produce an electric dipole moment that oscillates at a frequency corresponding to approximately twice the rotational constant of the molecule and couples to a nearby qubit. The four panels in (A) show the initial state |0;1〉 evolving through the gate to evolving through the gate to i|1;0|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array., where horizontal arrows indicate the flow of time. State |e|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array. of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array. to |e|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array. in the gate qubits, so that the amplitudes of the |0;e|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array. and |e;0|1;0〉, where horizontal arrows indicate the flow of time. State |e〉 of the storage qubits is light shifted out of resonance, for individual addressability. (B) Includes other basis states and important details of quantum phases. (C) Qubit array based on molecular hyperfine states. Any pair of qubits can be moved from the storage zone to the gate zone in a flexible array of optical tweezers. During the gate operation, a spatially uniform microwave pulse transfers population from state |1〉 to |e〉 in the gate qubits, so that the amplitudes of the |0;e〉 and |e;0〉 states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array. states are exchanged. To achieve individual addressability with high spatial resolution, the light that shifts the storage qubits out of resonance (indicated by red shadows) can be produced in a similar way as the tweezer array.

Fig. 2. Hyperfine and Zeeman energy levels as a function of magnetic field for the N = 1 (top) and N = 0 (bottom) states of ²³Na¹³³Cs (v = 0) in zero electric field. While a number of states are nearly degenerate with the states of interest |0 = 0) in zero electric field. While a number of states are nearly degenerate with the states of interest |0〉, |1〉, and |e〉, selection rules prevent them from participating in the interactions. , |1 = 0) in zero electric field. While a number of states are nearly degenerate with the states of interest |0〉, |1〉, and |e〉, selection rules prevent them from participating in the interactions. , and |e = 0) in zero electric field. While a number of states are nearly degenerate with the states of interest |0〉, |1〉, and |e〉, selection rules prevent them from participating in the interactions. , selection rules prevent them from participating in the interactions. B_v = 1.7396 GHz is the molecular rotation constant.

Fig. 3. Loss of fidelity as a function of duration for the two π-pulses (2 – F_π1 – F_π2) and exchange (1 – F_x). In both cases, the interaction strength (drive strength or molecule–molecule separation) is adjusted so the operation completes in the nominal duration. The ripples are caused by the square pulse shape whose sinc-function power-spectrum-minima move across off-resonant transitions as the duration is varied. The scaling behavior for the maximum fidelity points is 2 – F_π1 – F_π2 = 2.8 × 10^–4t^–2 and 1 – F_x = 8.5 × 10^–5t^–2 where t is given in ms. Details of the fidelity calculation are given in Section 4. The solid lines represent the perturbation theory results while the dotted lines correspond to the full Hamiltonian.

Fig. 4. Differential light shifts of excited rotational states (N = 1) with respect to the ground state, as a function of trap depth. The large offset of about 3.48 GHz has been subtracted. States with predominantly character with dipole moment along x[combining circumflex] are shown in black. States with predominantly character with dipole moment along ŷ are blue. States with predominantly |m_N = 0 = 0〉 character with dipole moment along character with dipole moment along ẑ are red. The thick line shows the state |e are red. The thick line shows the state |e〉 = |1,−1,3/2,7/2〉. The polarization vector is = |1,–1,3/2,7/2 are red. The thick line shows the state |e〉 = |1,−1,3/2,7/2〉. The polarization vector is . The polarization vector is ε̂ = x[combining circumflex] cos γ + iŷ sin γ with ellipticity γ = 35.6091°, adjusted to null the slope of |e = 35.6091°, adjusted to null the slope of |e〉 at 600 kHz. A magnetic field of 35 Gauss lies along at 600 kHz. A magnetic field of 35 Gauss lies along ẑ.

Fig. 5. Off-resonant coupling terms |Ω_ij/δ_ij| that cause population leakage during the gate steps. Here, Ω_ij is the coupling Rabi rate between source state i and leakage state j, and δ_ij is the frequency difference in radians per s. For each step, the probability of population leakage p_i is shown (see Appendix A), where the summation is over all coupled states j. p_i can be used to estimate off-resonant population leakage without calculating the full unitary time evolution. (A) Exchange interaction with separation of 2.5 μm along x[combining circumflex] for a 2 ms exchange duration. The fidelity, calculated from unitary time evolution is F = 1 – 2.0 × 10^–6. (B) |1. (B) |1〉 ↔ |e〉 π-pulse with electric field amplitude 0.0544 V m ↔ |e. (B) |1〉 ↔ |e〉 π-pulse with electric field amplitude 0.0544 V m π-pulse with electric field amplitude 0.0544 V m^–1 along ẑ for a 3.12 ms pulse duration. The fidelity for a pair of π-pulses, calculated from the unitary time evolution is F = 1 – 5.4 × 10^–5. (C) |0. (C) |0〉 ↔ |e〉 π-pulse with electric field amplitude 0.0157 V m ↔ |e. (C) |0〉 ↔ |e〉 π-pulse with electric field amplitude 0.0157 V m π-pulse with electric field amplitude 0.0157 V m^–1 along x[combining circumflex] for a 1.233 ms pulse duration. The state |1 for a 1.233 ms pulse duration. The state |1〉 can be neglected if its population has already been transferred to |e〉. can be neglected if its population has already been transferred to |e for a 1.233 ms pulse duration. The state |1〉 can be neglected if its population has already been transferred to |e〉..