Mathematical modeling of circadian rhythms

Abstract

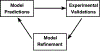
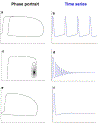
Circadian rhythms are endogenous ~24-hr oscillations usually entrained to daily environmental cycles of light/dark. Many biological processes and physiological functions including mammalian body temperature, the cell cycle, sleep/wake cycles, neurobehavioral performance, and a wide range of diseases including metabolic, cardiovascular, and psychiatric disorders are impacted by these rhythms. Circadian clocks are present within individual cells and at tissue and organismal levels as emergent properties from the interaction of cellular oscillators. Mathematical models of circadian rhythms have been proposed to provide a better understanding of and to predict aspects of this complex physiological system. These models can be used to: (a) manipulate the system in silico with specificity that cannot be easily achieved using in vivo and in vitro experimental methods and at lower cost, (b) resolve apparently contradictory empirical results, (c) generate hypotheses, (d) design new experiments, and (e) to design interventions for altering circadian rhythms. Mathematical models differ in structure, the underlying assumptions, the number of parameters and variables, and constraints on variables. Models representing circadian rhythms at different physiologic scales and in different species are reviewed to promote understanding of these models and facilitate their use. This article is categorized under: Physiology > Mammalian Physiology in Health and Disease Models of Systems Properties and Processes > Organ, Tissue, and Physiological Models.

Keywords: biological oscillators; circadian clock; circadian rhythms; dynamic systems; mathematical modeling; statistical modeling.

Fig.1.

An iterative process of model validation.

Fig.2.

Illustrative examples of self-sustained (a & b), damped (c & d), and excitable (e & f) oscillations for the Hodgkin-Huxley model of a neuron, with variation in the potassium channel conductivity parameter. The left column shows the phase portraits (i.e., how 2 variables evolve in time with respect to each other. Note that time is an implicit variable), while the right column shows how one variable (voltage) changes with time. For the self-sustained oscillator (a, b), the model evolves to a closed limit cycle with a periodic output. For the damped oscillator (c, d), the model evolves to a steady state as the amplitude of the oscillation decays. For the excitable oscillator (e, f), a single cycle can be evoked, but the system thereafter returns to the steady state.

Fig. 3.

A schematic description of one method for developing a mathematical model. (Revised from the schema in (Brown & Luithardt, 1999; Klerman & St Hilaire, 2007).