Knowledge gaps in the early growth of semantic feature networks
- PMID: 30333998
- PMCID: PMC6186390
- DOI: 10.1038/s41562-018-0422-4
Knowledge gaps in the early growth of semantic feature networks
Abstract
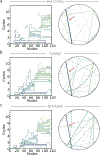
Understanding language learning, and more general knowledge acquisition, requires characterization of inherently qualitative structures. Recent work has applied network science to this task by creating semantic feature networks, in which words correspond to nodes and connections to shared features, then characterizing the structure of strongly inter-related groups of words. However, the importance of sparse portions of the semantic network - knowledge gaps - remains unexplored. Using applied topology we query the prevalence of knowledge gaps, which we propose manifest as cavities within the growing semantic feature network of toddlers. We detect topological cavities of multiple dimensions and find that despite word order variation, global organization remains similar. We also show that nodal network measures correlate with filling cavities better than basic lexical properties. Finally, we discuss the importance of semantic feature network topology in language learning and speculate that the progression through knowledge gaps may be a robust feature of knowledge acquisition.
Conflict of interest statement
Competing Interests The authors declare no competing interests.
Figures
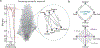


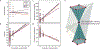

References
-
- Duff Fiona J and Hulme Charles. The role of children’s phonological and semantic knowledge in learning to read words. Scientific Studies of Reading, 16(6):504–525, 2012.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

