Forget-me-some: General versus special purpose models in a hierarchical probabilistic task

Abstract

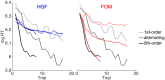
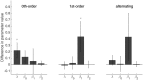
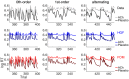
Humans build models of their environments and act according to what they have learnt. In simple experimental environments, such model-based behaviour is often well accounted for as if subjects are ideal Bayesian observers. However, more complex probabilistic tasks require more sophisticated forms of inference that are sufficiently computationally and statistically taxing as to demand approximation. Here, we study properties of two approximation schemes in the context of a serial reaction time task in which stimuli were generated from a hierarchical Markov chain. One, pre-existing, scheme was a generically powerful variational method for hierarchical inference which has recently become popular as an account of psychological and neural data across a wide swathe of probabilistic tasks. A second, novel, scheme was more specifically tailored to the task at hand. We show that the latter model fit significantly better than the former. This suggests that our subjects were sensitive to many of the particular constraints of a complex behavioural task. Further, the tailored model provided a different perspective on the effects of cholinergic manipulations in the task. Neither model fit the behaviour on more complex contingencies that competently. These results illustrate the benefits and challenges that come with the general and special purpose modelling approaches and raise important questions of how they can advance our current understanding of learning mechanisms in the brain.

Fig 1. Transition matrices T’s used to generate stimulus sequences within contextual blocks.

Over the course of the experiment, four 0^th-order sequences, two 1^st-order sequences and two alternating sequences occurred, three times each. Here, as is conventional for Markov chains, we show each ${\mathcal{T}}_{ij}$ as p(s^t = j|s^t−1 = i) (which is the transpose of the way the transitions were shown in [13]). The different dynamics of the matrices are illustrated by example sequences generated from each of the three matrix types (i.e. from matrices 1, 3 and 4 in the upper row).

Fig 2. Example sequences for the 0^th-order sequences: Experimental data (black), and predictions for the original (purple) and relaxed HGF (blue) and the FOM (red) averaged over subjects in the placebo group.

High probability transitions from stimulus 2 to 2 are shaded in grey. The stimulus sequence is shown underneath the lines.

Fig 3. Model fits to the 0^th-order sequences.

RTs in the placebo group are shown in black and predictions of the HGF in blue and FOM in red. (a) Distribution of average RTs and predictions. (b) Estimates of the probability for transition from stimulus 2 to 2 (shaded grey) in the sequence shown in Fig 2 simulated from the average parameters inferred from the placebo group. The horizontal lines indicate uniform belief (0.25) and the transition probability of the predominant transition (0.7) of the transition from stimulus 2 to the next stimulus. (c) RTs and model predictions averaged over all uninterrupted sequences of the high probability stimulus separated according to whether they started in the first or second half of blocks. Trials on which the speeding curve was significantly shallower during the second half compared to the first are marked by asterisks.

Fig 4. Forgetful Observer Model (FOM).

The perceptual component tracks the observers’ learning over just two levels. The lower level represents transition probabilities analogous to the generating transition matrices $\mathcal{T}$’s. The top level represents the parameters of a (forgetful) Dirichlet distribution. These can be interpreted as counting numbers of effective transitions, which are incremented by experience, and decremented to an asymptotic prior γ by a forgetting rate λ. The response component predicts subjects’ responses according to a linear combination (with weights β) of quantities in the perceptual component and model-agnostic factors.

Fig 5. Example sequences for the 1^st-order and alternating sequences.

Shown are the data (black), and predictions for the HGF (blue) and the FOM (red) averaged over subjects in the placebo group. High probability transitions are shaded in grey.

Fig 6. Speeding on high probability sequences for different matrix types.

RTs (grey) and predictions of the HGF (blue) and FOM (red) averaged over subjects in the placebo group for all uniterrupted sequences of high probability transitions for the three matrix types.

Fig 7. Response variability in sequences of high probability transitions.

Average RTs in placebo group (grey) for a single example sequence of high probability transitions in a 1^st-order and alternating context, and predictions of the FOM (red).

Fig 8. Differences in parameter values of ACh groups versus placebo for different matrix types.

ACh group shows a significantly higher forgetting rate and average response time for FOM fitted on 0^th-order matrices only, whereas FOM fitted to either 1^st or alternating matrices show significantly less response modulation. Error bars indicate 95%-confidence intervals; significance stars indicate significance from zero after Bonferroni correction.

Fig 9. Comparison of actual and predicted responses between placebo and ACh group.

Average RTs in placebo and ACh group (grey) for one example block from each of the three types and average predictions of HGF (blue) and FOM (red).