Automatically Selecting a Suitable Integration Scheme for Systems of Differential Equations in Neuron Models

Abstract

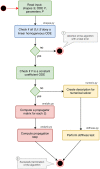
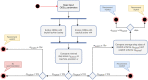
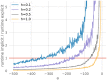
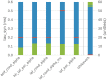
On the level of the spiking activity, the integrate-and-fire neuron is one of the most commonly used descriptions of neural activity. A multitude of variants has been proposed to cope with the huge diversity of behaviors observed in biological nerve cells. The main appeal of this class of model is that it can be defined in terms of a hybrid model, where a set of mathematical equations describes the sub-threshold dynamics of the membrane potential and the generation of action potentials is often only added algorithmically without the shape of spikes being part of the equations. In contrast to more detailed biophysical models, this simple description of neuron models allows the routine simulation of large biological neuronal networks on standard hardware widely available in most laboratories these days. The time evolution of the relevant state variables is usually defined by a small set of ordinary differential equations (ODEs). A small number of evolution schemes for the corresponding systems of ODEs are commonly used for many neuron models, and form the basis of the neuron model implementations built into commonly used simulators like Brian, NEST and NEURON. However, an often neglected problem is that the implemented evolution schemes are only rarely selected through a structured process based on numerical criteria. This practice cannot guarantee accurate and stable solutions for the equations and the actual quality of the solution depends largely on the parametrization of the model. In this article, we give an overview of typical equations and state descriptions for the dynamics of the relevant variables in integrate-and-fire models. We then describe a formal mathematical process to automate the design or selection of a suitable evolution scheme for this large class of models. Finally, we present the reference implementation of our symbolic analysis toolbox for ODEs that can guide modelers during the implementation of custom neuron models.

Keywords: ODE; integrate-and-fire neuron; integration schemes; model dynamics; numerics; symbolic analysis.

Figure 1

Activity diagram summarizing all steps of the ODE analysis algorithm. Steps executed in the main script of the toolbox are shown in green. The analysis of postsynaptic shapes (blue box) is detailed in section 3.1. Parts shown in red represent the generation of an analytical solver, which is described in section 3.2. The selection of a numerical stepper function is carried out by the yellow actions and explained in section 3.3.

Figure 2

Activity diagram summarizing the steps taken to recommend an appropriate numerical stepping scheme. The input to the algorithm are the ODEs and their parameters. After evolving the system of ODEs in parallel with an implicit and an explicit solver, it compares the minimal step sizes (m_scheme) of each scheme with the machine precision (ε). Depending on the outcome of the comparison, it recommends an appropriate stepping scheme (explicit or implicit) or compares the average step sizes (s_scheme) of the tested schemes. In the case that both the step size of the explicit and implicit solver are close to ε, the algorithm does not give a recommendation, but terminates with a warning instead.

Figure 3

Comparison of implicit and explicit methods for a stiff ODE. Ratio of runtimes for the implicit and explicit method as a function of the factor a in equation 20, for varying resolutions h and a desired accuracy of 10⁻³. Curves averaged over 5 runs of 20 ms each. The red bar indicates when the explicit and implicit methods require the same amount of time to evolve the ODE system. Where a curve is below the red bar, the implicit method is faster than the corresponding explicit method.

Listing 1

Example JSON file as input to the analysis toolbox. The file contains three entries: odes describing the ODEs of the system, shapes containing the postsynaptic shapes used in the ODEs and parameters specifying the parameters and default values for the differential equations in the shapes and odes sections.

Figure 4

Results of the stiffness test for six neuron models from NEST. Red bars indicate the default value of the selected parameter in NEST, blue indicates the value range in which the system of ODEs evaluates as non-stiff, green indicates the range in which it evaluates as stiff. aeif_cond_alpha is a conductance-based adaptive exponential integrate-and-fire model with alpha-shaped postsynaptic conductances, hh_psc_alpha a Hodgkin-Huxley type model with alpha-shaped postsynaptic currents, iaf_cond_alpha a conductance-based integrate-and-fire neuron with alpha-shaped postsynaptic conductances, iaf_cond_alpha_mc a conductance-based integrate-and-fire neuron with alpha-shaped postsynaptic conductances and multiple compartments, iaf_psc_alpha a current-based integrate-and-fire neuron with alpha-shaped postsynaptic currents and izhikevich the model dynamics proposed by Izhikevich (2003). The test was applied to the ODE systems for varying values of the parameter tau_syn of the first five models and for the parameter a of the last model.

Figure 5

Application of the stiffness tester to the Fitzhugh-Nagumo model. Ratio of runtimes for the implicit and explicit method as a function of the factor τ in equation 21, for varying resolution h and a desired accuracy of 10⁻⁵. Curves averaged over 5 runs of 20 ms each. Red bar as in Figure 3.

Figure 6

Application of the stiffness tester to the Morris-Lecar model. Ratio of runtimes for the implicit and explicit method as a function of the factor ε in equation 22, for varying resolution h and a desired accuracy of 10⁻⁵. Curves averaged over 5 runs of 20 ms each. Red bar as in Figure 3.