Multipartite Entanglement at Finite Temperature

Abstract

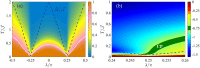
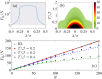
The interplay of quantum and thermal fluctuations in the vicinity of a quantum critical point characterizes the physics of strongly correlated systems. Here we investigate this interplay from a quantum information perspective presenting the universal phase diagram of the quantum Fisher information at a quantum phase transition. Different regions in the diagram are identified by characteristic scaling laws of the quantum Fisher information with respect to temperature. This feature has immediate consequences on the thermal robustness of quantum coherence and multipartite entanglement. We support the theoretical predictions with the analysis of paradigmatic spin systems showing symmetry-breaking quantum phase transitions and free-fermion models characterized by topological phases. In particular we show that topological systems are characterized by the survival of large multipartite entanglement, reaching the Heisenberg limit at finite temperature.

Figure 1

Schematic general behavior of the scaling of the QFI in the vicinity of a critical point. Control parameter λ versus temperature T for the QFI of a critical many-body system. We distinguish four regions depending on the scaling exponent β = d log F_Q/d log T of the QFI with respect to temperature: a quantum plateau (QP), a thermal plateau (TP), a critical plateau (CP) and a maximum entropy plateau (MEP). QP and TP are defined from the lower bound Eq. (1), showing that the QFI remains at least constant (β ≥ 0) up to a crossover temperature T_cross (white solid line) of the order of the first nonvanishing gap Δ in the energy spectrum (dashed line). The characteristic feature of the TP region is the degeneracy of the ground state: in the thermodynamic limit, the QFI suddenly decreases from its value at T = 0 to the plateau value. In the CP, the QFI follows a scaling law controlled by critical exponents of the model, β = −Δ_Q/z, according to Eq. (4). For temperatures larger than T_max (dotted line) – approximatively equal to the maximum energy of the spectrum – the QFI enters the MEP where β = −2. In the crossover grey regions the thermal decay is non-universal.

Figure 2

Bounds of the QFI. For unitary phase-encoding transformations, $F_Q[\hat{\rho },\hat{O}]=0$ if and only if the state is incoherent. Among quantum coherent states, $F_Q[\hat{\rho },\hat{O}]>0$, we can find bounds to the QFI depending on the entanglement properties of the state: $F_Q[\hat{\rho },\hat{O}]\le b_1$ for separable states [orange region, where b₁ is also indicated as shot-noise (SN) limit], $F_Q[\hat{\rho },\hat{O}]\le b_{\kappa }$ for κ-partite entangled states with 1 ≤ κ ≤ N − 1 [green region], and $F_Q[\hat{\rho },\hat{O}]\le b_N$ for all possible states [where b_N is also indicated as Heisenberg limit (HL)]. The bounds b_κ depend, in general, on the operator $\hat{O}$.

Figure 3

Phase diagram of the BJJ model. (a) QFI normalized to its low-temperature value, $F_Q[{\hat{\rho }}_T]/F_Q[{\hat{\rho }}_0]$ (color scale) as a function of λ and T. The region where the low-temperature behavior survives is highlighted by the orange color. The black dotted line at $\lambda \approx \mathrm{atan}\left(\mathrm{1/}\sqrt{2}\right)$ separates the regions where the optimal parameter is ${\hat{S}}_x$ (on the left) and ${\hat{S}}_z$ (on the right). (b) Scaling coefficient $\beta =d\log F_Q[{\hat{\rho }}_T]/d\log T$ (color scale) as a function of λ and T. The dotted line is the upper bound of the spectrum, ${\max }_n{E}_n$. The inset shows β as a function of T at λ/π = 0.4: the different plateaus are clearly visible. In both panels N = 2000, the solid white curve is the crossover temperature T_cross(λ) following the energy gaps Δ₁ (dashed blue line) and Δ₂ (dashed red line).

Figure 4

QFI for the BJJ model. (a) Fisher density F_Q[|ψ₀〉]/N (blue line) and inverse spin-squeezing parameter 1/ξ² (orange line) as a function of λ for the ground state of Eq. (26). The two lines superpose for $\lambda \gtrsim {\lambda }_{\mathrm{c}}$. The vertical dashed line signals the critical point λ_c = π/4. Panels (b and c) show the Fisher density $F_Q[{\hat{\rho }}_T]/N$ (dots) as a function of T for (b) λ = 0.3π > λ_c and (c) λ = 0.24π < λ_c. Solid lines are analytical curves, Eqs (30) and (34), for different values of the cutoff k. The vertical dashed lines indicates T = Δ_1,2. In panels (a–c) the shaded area indicates multipartite entanglement F_Q/N > 1. (d) Fisher density $F_Q[{\hat{\rho }}_T]/N$ (color scale) in the λ-T phase diagram. Multipartite entanglement is witnessed at nonzero temperature in the colored region, where $F_Q[{\hat{\rho }}_T]/N>1$, while $F_Q[{\hat{\rho }}_T]/N\le 1$ corresponds to the white region. The dashed line is the analytical boundary of $F_Q[{\hat{\rho }}_T]=N$ in the thermodynamic limit, given by Eq. (36) for λ > λ_c and Eq. (37) for λ < λ_c. In all the panels, numerical data are obtained for N = 2000.

Figure 5

Phase diagram of the Ising model in transverse field. (a) QFI normalized to its low-temperature value, $F_Q[{\hat{\rho }}_T]/F_Q[{\hat{\rho }}_0]$ (color scale), in the λ-T phase diagram. (b) Scaling coefficient $\beta =d\log F_Q[{\hat{\rho }}_T]/d\log T$ in the vicinity of the critical point. In both panels, the white solid line is the crossover temperature T_cross(λ). The blue and red dashed lines indicate Δ₁ and Δ₂, respectively. In both panels, N = 50.

Figure 6

QFI for the Ising model in transverse field. (a) Fisher density F_Q[|ψ₀〉]/N (blue line) and inverse spin squeezing (orange line) for the ground state of Eq. (39) as a function of λ. The vertical dashed line signals the critical point λ_c. Panels (b and c) show the typical decay of the Fisher density $F_Q[{\hat{\rho }}_T]/N$ as a function of T in the paramagnetic (b) and ferromagnetic (c) phase. The solid lines are ${\tanh }^2({\mathrm{\Delta }}_1\mathrm{/2}T)$ or ${\tanh }^2({\mathrm{\Delta }}_2\mathrm{/2}T)$. In panels (a–c) the shaded area indicates multipartite entanglement. (d) Fisher density $F_Q[{\hat{\rho }}_T]/N$ (color scale) in the λ-T phase diagram. The dashed line is the spin-squeezing boundary ξ² = 1. In all panels N = 50.

Figure 7

Phase diagram of the Kitaev chain with short-range pairing. (a) QFI normalized to its low-temperature value, $F_Q[{\hat{\rho }}_T]/F_Q[|{\psi }_0\rangle ]$ (color scale), in the λ-T phase diagram. (b) Scaling coefficient $\beta =d\log F_Q[{\hat{\rho }}_T]/d\log T$ as a function of λ and T. In both panels the white line is T_cross and the blue dashed line is the energy gap Δ. Here N = 50 and α = 100.

Figure 8

QFI for the Kitaev chain with short-range pairing. (a) Fisher density F_Q[|ψ₀〉]/N as a function of λ for the ground state of Eq. (44) with N = 50 and α = 100. The vertical dashed lines signal the critical points λ_c. The shaded area marks entanglement, F_Q[|ψ₀〉] > N. (b) Fisher density $F_Q[{\hat{\rho }}_T]/N$ (color scale) in the λ-T plane for N = 50. The colored area corresponds to $F_Q[{\hat{\rho }}_T]>N$. (c) Scaling of $F_Q[{\hat{\rho }}_T]/N$ as a function of N for different temperatures. The thick black line is the Heisenberg limit F_Q = N², the dashed lines are the bound in Eq. (45).

Figure 9

Phase diagram of the Kitaev chain with long-range pairing. (a) QFI normalized to its low-temperature value, $F_Q[{\hat{\rho }}_T]/F_Q[|{\psi }_0\rangle ]$ (color scale), in the λ-T phase diagram. (b) Scaling coefficient $\beta =d\log F_Q[{\hat{\rho }}_T]/d\log T$. In both panels the white line is T_cross and the blue dashed line is the energy gap Δ. Here N = 50 and α = 0.

Figure 10

QFI for the Kitaev chain with long-range pairing. (a) Fisher density F_Q[|ψ₀〉]/N as a function of λ for the ground state of Eq. (44) with N = 50 and α = 0. The QFI is calculated using both the operators ${\hat{O}}_x^{+}$ (dark blue line) and ${\hat{O}}_y^{(-)}$ (light blue line). The vertical dashed line signals the critical point λ_c, while the shaded area marks multipartite entanglement. (b) Fisher density $F_Q[{\hat{\rho }}_T]/N$ (color scale) in the λ-T plane for N = 50. (c) Scaling of $F_Q[{\hat{\rho }}_T]/N$ for increasing N. The dashed lines are Eq. (45) for different values of T.