Going Beyond the Data as the Patching (Sheaving) of Local Knowledge

Abstract

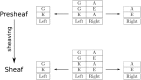
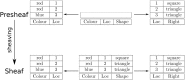
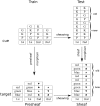
Consistently predicting outcomes in novel situations is colloquially called "going beyond the data," or "generalization." Going beyond the data features in spatial and non-spatial cognition, raising the question of whether such features have a common basis-a kind of systematicity of generalization. Here, we conceptualize this ability as the patching of local knowledge to obtain non-local (global) information. Tracking the passage from local to global properties is the purview of sheaf theory, a branch of mathematics at the nexus of algebra and geometry/topology. Two cognitive domains are examined: (1) learning cue-target patterns that conform to an underlying algebraic rule, and (2) visual attention requiring the integration of space-based feature maps. In both cases, going beyond the data is obtained from a (universal) sheaf theory construction called "sheaving," i.e., the "patching" of local data attached to a topological space to obtain a representation considered as a globally coherent cognitive map. These results are discussed in the context of a previous (category theory) explanation for systematicity, vis-a-vis, categorical universal constructions, along with other cognitive domains where going beyond the data is apparent. Analogous to higher-order function (i.e., a function that takes/returns a function), going beyond the data as a higher-order systematicity property is explained by sheaving, a higher-order (categorical) universal construction.

Keywords: category theory; generalization; learning; sheaf; sheaf theory; sheaving; universal.

Figure 1

An example of sheaving as a product.

Figure 2

An example of sheaving as a constrained product (empty box indicates empty set).

Figure 3

An example of generalization as sheaving.