Going with the Flow: Multiscale Insights into the Composite Nature of Water Transport in Roots

Abstract

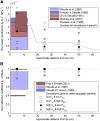
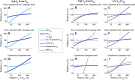
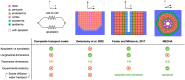
As water often limits crop production, a more complete understanding of plant water capture and transport is necessary. Here, we developed MECHA, a mathematical model that computes the flow of water across the root at the scale of walls, membranes, and plasmodesmata of individual cells, and used it to test hypotheses related to root water transport in maize (Zea mays). The model uses detailed root anatomical descriptions and a minimal set of experimental cell properties, including the conductivity of plasma membranes, cell walls, and plasmodesmata, which yield quantitative and scale-consistent estimations of water pathways and root radial hydraulic conductivity (k _r). MECHA revealed that the mainstream hydraulic theories derived independently at the cell and root segment scales are compatible only if osmotic potentials within the apoplastic domains are uniform. The results suggested that the convection-diffusion of apoplastic solutes explained most of the offset between estimated k _r in pressure clamp and osmotic experiments, while the contribution of water-filled intercellular spaces was limited. Furthermore, sensitivity analyses quantified the relative impact of cortex and endodermis cell conductivity of plasma membranes on root k _r and suggested that only the latter contributed substantially to k _r due to the composite nature of water flow across roots. The explicit root hydraulic anatomy framework brings insights into contradictory interpretations of experiments from the literature and suggests experiments to efficiently address questions pertaining to root water relations. Its scale consistency opens avenues for cross-scale communication in the world of root hydraulics.

Figure 1.

Overview scheme of the root cross-section hydraulic anatomy approach. A transverse root microscope image (A) is treated through CellSet (C) to create the anatomical layout for cell-scale hydraulic principles (D). When coupled to cell-scale hydraulic properties (B), they form the root hydraulic anatomy (E). The computed water flow rates across individual cells (F) also yield the root radial conductivity and reflection coefficient (G).

Figure 2.

Comparison of root radial hydraulic properties measured and simulated for various cell-scale hydraulic properties along a root. The three simulated distances from the tip correspond to different levels of apoplastic barrier development: endodermal Casparian strip (5 cm), suberized endodermis with passage cells (25 cm), and suberized endodermis and exodermal Casparian strip (50 cm). A, Comparison between experimental k_r ranges in maize primary roots (colored rectangles and dashed line) and k_r simulated from the cell scale in the maize hydraulic anatomy (consistent symbols across legends with impermeable and leaky apoplastic barriers in black and gray, respectively). B, Comparison between experimental mannitol σ_r ranges in maize principal roots (colored rectangles) and root segment σ_r arising from the cell scale in the maize hydraulic anatomy (σ_r values lower than 1 were obtained with the water-permeable apoplastic barrier).

Figure 3.

Impact of solute radial convection-diffusion in the apoplast on the estimations of maize root radial conductivity in simulated osmotic and pressure clamp experiments for high k_w and low K_PD. A, Steady-state apoplastic osmotic potentials simulated when increasing the xylem pressure by incremental pressure clamps of 0.025 MPa for a solute diffusivity of 4 × 10⁻¹¹ m² s⁻¹ (colored curves) and an infinite diffusivity (black curves). B, Steady-state radial water fluxes simulated in response to the incremental pressure clamps of 0.025 MPa for four levels of solute diffusivity. C, Steady-state apoplastic osmotic potentials simulated after adding mannitol in the root bathing solution by increments of 10 mosmol for a solute diffusivity of 4 × 10⁻¹¹ m² s⁻¹ (colored curves) and an infinite diffusivity (black curves). D, Steady-state radial water fluxes simulated in response to the increments of 10 mosmol in the bathing solution for four levels of solute diffusivity.

Figure 4.

Relative radial hydraulic conductivity as a function of specific relative cell hydraulic conductivities. Relationships are shown for the fully suberized endodermis with an extra exodermal Casparian band (A–C), the suberized endodermis with three passage cells (D–F), and the simple endodermal Casparian band stage (G–I). In A, D, and G, cell properties (L_p in blue or K_PD in cyan) were altered simultaneously in all tissue types, while in other graphs, L_p was modified in specific tissue types (in epidermis and exodermis in dashed light blue, cortex in solid blue, endodermis in dashed dark blue, and stele cells in solid black). Graphs B, E, and H and C, F, and I have high and low cell wall hydraulic conductivities, respectively, and low K_PD (Table 2).

Figure 5.

Scheme comparing major approaches to simulate water flow across root tissues. The nonexhaustive criteria listed are the separation of apoplastic and symplastic pathways, the number of dimensions attributed to the representation of longitudinally and transversely varying root properties, the compatibility with experimental anatomical layouts, and the tight coupling between solute radial distribution and water flow.

Figure 6.

From anatomical segmentation to water flow simulation with CellSet and MECHA. A, Maize root cross section with exodermis after segmentation in CellSet. Successive cellular tissue types from the periphery are epidermis, exodermis, cortex, endodermis, pericycle, and other stele cells. Water potential boundary conditions were set at the epidermis surface and in xylem vessels (dark green). Bar = 100 µm. B, Simulated water fluxes in cell walls, in m s⁻¹, combining impermeable apoplastic barriers with high k_w, low K_PD hydraulic properties, and 0.5 MPa water potential difference between the root surface and xylem, generating an average uptake flux at the root surface of 2 × 10⁻⁸ m s⁻¹. Note that cell wall thickness is exaggerated to improve the visualization.