A flexible likelihood approach for predicting neural spiking activity from oscillatory phase
- PMID: 30367887
- PMCID: PMC6387742
- DOI: 10.1016/j.jneumeth.2018.10.028
A flexible likelihood approach for predicting neural spiking activity from oscillatory phase
Abstract
Background: The synchronous ionic currents that give rise to neural oscillations have complex influences on neuronal spiking activity that are challenging to characterize.
New method: Here we present a method to estimate probabilistic relationships between neural spiking activity and the phase of field oscillations using a generalized linear model (GLM) with an overcomplete basis of circular functions. We first use an L1-regularized maximum likelihood procedure to select an active set of regressors from the overcomplete set and perform model fitting using standard maximum likelihood estimation. An information theoretic model selection procedure is then used to identify an optimal subset of regressors and associated coefficients that minimize overfitting. To assess goodness of fit, we apply the time-rescaling theorem and compare model predictions to original data using quantile-quantile plots.
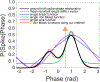
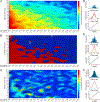
Results: Spike-phase relationships in synthetic data were robustly characterized. When applied to in vivo hippocampal data from an awake behaving rat, our method captured a multimodal relationship between the spiking activity of a CA1 interneuron, a theta (5-10 Hz) rhythm, and a nested high gamma (65-135 Hz) rhythm.
Comparison with existing methods: Previous methods for characterizing spike-phase relationships are often only suitable for unimodal relationships, impose specific relationship shapes, or have limited ability to assess the accuracy or fit of their characterizations.
Conclusions: This method advances the way spike-phase relationships are visualized and quantified, and captures multimodal spike-phase relationships, including relationships with multiple nested rhythms. Overall, our method is a powerful tool for revealing a wide range of neural circuit interactions.
Keywords: CA1; Gamma rhythm; Generalized linear model; Hippocampus; Interneuron; L1-regularization; Local field potential; Neural oscillations; Overcomplete basis; Point process modeling; Sparsity; Spike-phase relationship; Theta rhythm.
Copyright © 2018 The Author(s). Published by Elsevier B.V. All rights reserved.
Conflict of interest statement
Declarations of interest
None.
Figures

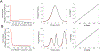


Similar articles
-
Modeling relationships between rhythmic processes and neuronal spike timing.J Neurophysiol. 2022 Sep 1;128(3):593-610. doi: 10.1152/jn.00423.2021. Epub 2022 Jul 20. J Neurophysiol. 2022. PMID: 35858125 Free PMC article.
-
Construction and analysis of non-Poisson stimulus-response models of neural spiking activity.J Neurosci Methods. 2001 Jan 30;105(1):25-37. doi: 10.1016/s0165-0270(00)00344-7. J Neurosci Methods. 2001. PMID: 11166363
-
Identification of time-varying neural dynamics from spike train data using multiwavelet basis functions.J Neurosci Methods. 2017 Feb 15;278:46-56. doi: 10.1016/j.jneumeth.2016.12.018. Epub 2017 Jan 4. J Neurosci Methods. 2017. PMID: 28062244
-
What is the function of hippocampal theta rhythm?--Linking behavioral data to phasic properties of field potential and unit recording data.Hippocampus. 2005;15(7):936-49. doi: 10.1002/hipo.20116. Hippocampus. 2005. PMID: 16158423 Review.
-
The contribution of electrical synapses to field potential oscillations in the hippocampal formation.Front Neural Circuits. 2014 Apr 3;8:32. doi: 10.3389/fncir.2014.00032. eCollection 2014. Front Neural Circuits. 2014. PMID: 24772068 Free PMC article. Review.
Cited by
-
Robust Regression and Optimal Transport Methods to Predict Gastrointestinal Disease Etiology From High Resolution EGG and Symptom Severity.IEEE Trans Biomed Eng. 2022 Nov;69(11):3313-3325. doi: 10.1109/TBME.2022.3167338. Epub 2022 Oct 19. IEEE Trans Biomed Eng. 2022. PMID: 35439119 Free PMC article.
-
Modeling relationships between rhythmic processes and neuronal spike timing.J Neurophysiol. 2022 Sep 1;128(3):593-610. doi: 10.1152/jn.00423.2021. Epub 2022 Jul 20. J Neurophysiol. 2022. PMID: 35858125 Free PMC article.
References
-
- Akaike H, 1974. A new look at the statistical model identification. IEEE Trans. Autom. Control 19 (6), 716–723.
-
- Barbieri R, Frank LM, Quirk MC, Solo V, Wilson MA, Brown EN, 2002. Construction and analysis of non-Gaussian spatial models of neural spiking activity. Neurocomputing 44, 309–314.
-
- Barbieri R, Quirk MC, Frank LM, Wilson MA, Brown EN, 2001. Construction and analysis of non-Poisson stimulus-response models of neural spiking activity. J. Neurosci. Methods 105 (1), 25–37. - PubMed
-
- Belloni A, Chernozhukov V, et al., 2013. Least squares after model selection in high-dimensional sparse models. Bernoulli 19 (2), 521–547.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

