A constructive approach to the epistemological problem of emergence in complex systems

Abstract

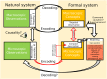
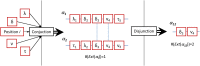
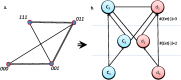
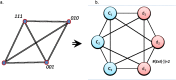
Emergent patterns in complex systems are related with many intriguing phenomena in modern science. One question that has sparked vigorous debates is if difficulties in the modelization of emergent behaviours are a consequence of ontological or epistemological limitations. To elucidate this question, we propose a novel approximation through constructive logic. Under this framework, experimental measurements will be considered conceptual building blocks from which we aim to achieve a description of the microstates ensemble mapping the macroscopic emergent observation. This procedure allow us to have full control of any information loss, thus making the analysis of different systems fairly comparable. In particular, we aim to look for compact descriptions of the constraints underlying a dynamical system, as a necessary a priori step to develop explanatory (mechanistic) models. We apply our proposal to a synthetic system to show that the number and scope of the system's constraints hinder our ability to build compact descriptions, being those systems under global constraints a limiting case in which such a description is unreachable. This result clearly links the epistemological limits of the framework selected with an ontological feature of the system, leading us to propose a definition of emergence strength which we make compatible with the scientific method through the active intervention of the observer on the system, following the spirit of Granger causality. We think that our approximation clarifies previous discrepancies found in the literature, reconciles distinct attempts to classify emergent processes, and paves the way to understand other challenging concepts such as downward causation.

Fig 1. Scheme of the epistemological approximation of an observer in the analysis of emergent properties.

Research starts with the observation of an emergent macroscopic property E and the associated ensemble of microstates M, both characterized through measurements. These observations are then encoded to build a formal framework. In this work, we are interested in finding a minimal epistemological map between the formal macroscopic and microscopic descriptions (red arrows). This map consists of finding a microscopic compact description of the ensemble, which is achieved through the identification of microscopic constraints in the dynamics of the system, in which case we will say that the macroscopic property is traceable. This is a necessary a priori step before a model is built (box modelling) that will allow the researcher to address other questions (see questions marks) such as supervenience of upper and lower level constituents or how to decode the formal framework under the scientific method through experiments. Interestingly, although we focus in a very specific epistemological process, and we do not explicitly address questions related with modelling or the ontology of emergent properties, the analysis of microscopic constraints sheds light over these questions.

Fig 2. Illustration of conjunction and disjunction of concepts.

Starting from the knowing subject’s conceptual apparatus (Greek letters, left), two sequences α₁ and α₂ are built through conjunction of the basic concepts, being themselves concepts (center). These sequences uniquely determine single objects, for instance protein sequences, and thus #(Ext(α_i)) = 1. Comparing both sequences we observe two common concepts (linked by dotted lines) that we identify through binary disjunction. If these two concepts are only found at these sequences, we can say that a new concept α₁₂ sharply describes these sequences (right). This concept contains less basic concepts, but the extension is larger than the original sequences, i.e. #(Ext(α₁₂)) = 2.

Fig 3. Illustration of disjunction of two concepts.

We consider two concepts α₁ and α₂, sharply defined by conjunction of red (ν₁ in the Main Text) and cyan (ν₂) for α₁, and by conjunction of red and green (ν₃) for α₂. The grey concepts denote any other colour needed to sharply determine the other α_i concepts. Since these three colours suffice to sharply describe α₁ and α₂, their extensions over the different objects of observation must follow one of the three general cases shown in the figure and described in the Main Text.

Fig 4. Representations of a three bits system with a single constraint of scope one.

(Left) In the concrete network, each node represents a microstate and it is linked with another microstate if they share the same observation for any component, where the number of links represent the number of concepts shared. (Right) Formal network of concepts extracted from the analysis of the microstates. Two links c_i and c_j are linked with a directed edge if Ext(c_i) ⊆ Ext(c_j) and with an undirected link if Ext(c_i) ∩ Ext(c_j) ≠ ∅. The concepts are hierarchically ordered according to the cardinality of their extension, i.e. the number of microstates they map. In this example, a single constraint on x₁ naturally arises, as one of its possible values maps the empty set.

Fig 5. Representations of a three bits system with two constraints of scope two.

(Left) In the concrete network, each node represents a microstate and it is linked with another microstate if they share the same observation for any component, where the number of links represent the number of concepts shared. (Right) Network of concepts extracted from the analysis of the microstates. Two links c_i and c_j are linked with a directed edge if Ext(c_i) ⊆ Ext(c_j) and with an undirected link if Ext(c_i) ∩ Ext(c_j) ≠ ∅. The concepts are hierarchically ordered according to the cardinality of their extension, i.e. the number of microstates they map. In this example we identify the constraints observing those links that, despite of being viable, are absent. For instance, there is no link between d₃ and c₂.

Fig 6. Representations of a three bits system with one constraint of scope three.

(Left) In the concrete network, each node represents a microstate and is linked with another microstate if they share the same observation for any component, where the number of links represent the number of concepts shared. (Right) Formal network of concepts extracted from the analysis of the microstates. Two links c_i and c_j are linked with a directed edge if Ext(c_i) ⊆ Ext(c_j) and with an undirected link if Ext(c_i) ∩ Ext(c_j) ≠ ∅. The graph of concepts is equivalent to the graph we would obtain for a free system, being just observed a reduction in the number of objects mapped by each concept (from #(Ext(⋅)) = 4 towards #(Ext(⋅)) = 2). It reflects the notion that the system has “no borders”.

Fig 7. Scheme illustrating the definition of coverage excess.

The scheme is divided in five columns (1-5) that we describe from left to right. (1) The 3-bit systems under analysis in the main text are shown. If we intervene in the systems neglecting one component (2) we will obtain a set of 2-bit states (3). For the system S1, removing x₁ lead to different states than if x₂ or x₃ are removed, while S2 and S3 lead to the same states independently of the component removed (see Main Text for details). From the 2-bit states, we recover the neglected component keeping it free of any constraint, which leads to a number of compatible 3-bit states (4). In the last column we show the result for the coverage excess obtained from this procedure using Eq 8. The final value for the coverage excess of the system will be the average among the values obtained from the different interventions.