Log-ratio lasso: Scalable, sparse estimation for log-ratio models
- PMID: 30387139
- PMCID: PMC9470385
- DOI: 10.1111/biom.12995
Log-ratio lasso: Scalable, sparse estimation for log-ratio models
Abstract
Positive-valued signal data is common in the biological and medical sciences, due to the prevalence of mass spectrometry other imaging techniques. With such data, only the relative intensities of the raw measurements are meaningful. It is desirable to consider models consisting of the log-ratios of all pairs of the raw features, since log-ratios are the simplest meaningful derived features. In this case, however, the dimensionality of the predictor space becomes large, and computationally efficient estimation procedures are required. In this work, we introduce an embedding of the log-ratio parameter space into a space of much lower dimension and use this representation to develop an efficient penalized fitting procedure. This procedure serves as the foundation for a two-step fitting procedure that combines a convex filtering step with a second non-convex pruning step to yield highly sparse solutions. On a cancer proteomics data set, the proposed method fits a highly sparse model consisting of features of known biological relevance while greatly improving upon the predictive accuracy of less interpretable methods.
Keywords: compositional data; lasso; log-ratio; mass spectrometry; variable selection.
© 2018 International Biometric Society.
Figures
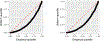

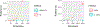
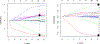
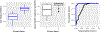
References
-
- Aitchison J (1982). The statistical analysis of compositional data. J R Stat Soc Ser B (Methodol) 44, 139–177.
-
- Aitchison J (1983). Principal component analysis of compositional data. Biometrika 70, 57–65.
-
- Aitchison J and Bacon-shone J (1984). Log contrast models for experiments with mixtures. Biometrika 71, 323–330.
-
- Akaike H (1974). A new look at the statistical model identification. IEEE Trans Autom Control 19, 716–723.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

