Effects of Passive Phospholipid Flip-Flop and Asymmetric External Fields on Bilayer Phase Equilibria
- PMID: 30393103
- PMCID: PMC6303420
- DOI: 10.1016/j.bpj.2018.10.003
Effects of Passive Phospholipid Flip-Flop and Asymmetric External Fields on Bilayer Phase Equilibria
Abstract
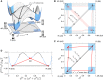
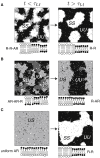
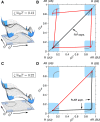
Compositional asymmetry between the leaflets of bilayer membranes modifies their phase behavior and is thought to influence other important features such as mechanical properties and protein activity. We address here how phase behavior is affected by passive phospholipid flip-flop, such that the compositional asymmetry is not fixed. We predict transitions from "pre-flip-flop" behavior to a restricted set of phase equilibria that can persist in the presence of passive flip-flop. Surprisingly, such states are not necessarily symmetric. We further account for external symmetry breaking, such as a preferential substrate interaction, and show how this can stabilize strongly asymmetric equilibrium states. Our theory explains several experimental observations of flip-flop-mediated changes in phase behavior and shows how domain formation and compositional asymmetry can be controlled in concert, by manipulating passive flip-flop rates and applying external fields.
Copyright © 2018 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures



Similar articles
-
Kinetics and thermodynamics of flip-flop in binary phospholipid membranes measured by sum-frequency vibrational spectroscopy.Biochemistry. 2009 Nov 3;48(43):10220-34. doi: 10.1021/bi901096j. Biochemistry. 2009. PMID: 19746969
-
The Ins and Outs of Lipid Flip-Flop.Acc Chem Res. 2017 Jan 17;50(1):58-65. doi: 10.1021/acs.accounts.6b00435. Epub 2016 Dec 13. Acc Chem Res. 2017. PMID: 27959517
-
Phospholipid flip-flop modulated by transmembrane peptides WALP and melittin.J Struct Biol. 2009 Oct;168(1):37-52. doi: 10.1016/j.jsb.2009.06.001. Epub 2009 Jun 7. J Struct Biol. 2009. PMID: 19508895 Free PMC article.
-
Chemical control of phospholipid distribution across bilayer membranes.Med Res Rev. 2002 May;22(3):251-81. doi: 10.1002/med.10009. Med Res Rev. 2002. PMID: 11933020 Review.
-
Evaluation of Interbilayer and Transbilayer Transfer Dynamics of Phospholipids Using Time-Resolved Small-Angle Neutron Scattering.Chem Pharm Bull (Tokyo). 2019;67(4):316-320. doi: 10.1248/cpb.c18-00942. Chem Pharm Bull (Tokyo). 2019. PMID: 30930434 Review.
Cited by
-
Experimentally determined leaflet-leaflet phase diagram of an asymmetric lipid bilayer.Proc Natl Acad Sci U S A. 2023 Nov 14;120(46):e2308723120. doi: 10.1073/pnas.2308723120. Epub 2023 Nov 8. Proc Natl Acad Sci U S A. 2023. PMID: 37939082 Free PMC article.
-
With Lipid Rafts, Context Is Everything.Biophys J. 2019 Nov 5;117(9):1549-1551. doi: 10.1016/j.bpj.2019.07.058. Epub 2019 Sep 25. Biophys J. 2019. PMID: 31604521 Free PMC article. No abstract available.
-
The Importance of Bilayer Asymmetry in Biological Membranes: Insights from Model Membranes.Membranes (Basel). 2025 Mar 3;15(3):79. doi: 10.3390/membranes15030079. Membranes (Basel). 2025. PMID: 40137031 Free PMC article. Review.
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

