Stochasticity in materials structure, properties, and processing-A review
- PMID: 30397419
- PMCID: PMC6214486
- DOI: 10.1063/1.4998144
Stochasticity in materials structure, properties, and processing-A review
Abstract
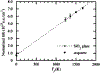
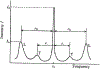
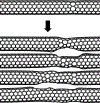
We review the concept of stochasticity-i.e., unpredictable or uncontrolled fluctuations in structure, chemistry, or kinetic processes-in materials. We first define six broad classes of stochasticity: equilibrium (thermodynamic) fluctuations; structural/compositional fluctuations; kinetic fluctuations; frustration and degeneracy; imprecision in measurements; and stochasticity in modeling and simulation. In this review, we focus on the first four classes that are inherent to materials phenomena. We next develop a mathematical framework for describing materials stochasticity and then show how it can be broadly applied to these four materials-related stochastic classes. In subsequent sections, we describe structural and compositional fluctuations at small length scales that modify material properties and behavior at larger length scales; systems with engineered fluctuations, concentrating primarily on composite materials; systems in which stochasticity is developed through nucleation and kinetic phenomena; and configurations in which constraints in a given system prevent it from attaining its ground state and cause it to attain several, equally likely (degenerate) states. We next describe how stochasticity in these processes results in variations in physical properties and how these variations are then accentuated by-or amplify-stochasticity in processing and manufacturing procedures. In summary, the origins of materials stochasticity, the degree to which it can be predicted and/or controlled, and the possibility of using stochastic descriptions of materials structure, properties, and processing as a new degree of freedom in materials design are described.
Figures
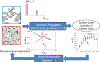

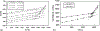








References
-
- See, for example, Bentley JP, “The accuracy of measurement systems in the steady state,” in Principles of Measurement Systems (Longman Scientific, Singapore, 1995), Chap. 3.
-
- See, for example, Hoffman D and Ernst F, Ultramicroscopy 53, 205(1994).
-
- See, for example, Kalinin SV, Strelcov E, Belianinov A, Somnath S, Vasudevan RK, Lingerfelt EJ, Archibald RK, Chen C, Proksch R, Laanait N, and Jesse S, ACS Nano 10, 9068 (2016). - PubMed
-
- Murphy JM, Sexton DM, Barnett DN, Jones GS, Webb MJ, Collins M, and Stainforth DA, Nature 430, 768 (2004). - PubMed
-
- Anisworth M and Oden JT, A Posteriori Error Estimation in Finite Element Analysis (John Wiley, 2000).
Grants and funding
LinkOut - more resources
Full Text Sources
