Interfacial Electric Effects on a Non-Isothermal Electroosmotic Flow in a Microcapillary Tube Filled by Two Immiscible Fluids

Abstract

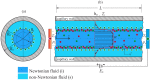
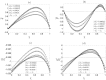
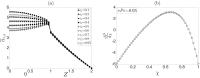
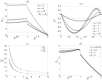
In this work, a non-isothermal electroosmotic flow of two immiscible fluids within a uniform microcapillary is theoretically studied. It is considered that there is an annular layer of a non-Newtonian liquid, whose behavior follows the power-law model, adjacent to the inside wall of the capillary, which in turn surrounds an inner flow of a second conducting liquid that is driven by electroosmosis. The inner fluid flow exerts an interfacial force, dragging the annular fluid due to shear and Maxwell stresses at the interface between the two fluids. Because the Joule heating effect may be present in electroosmotic flow (EOF), temperature gradients can appear along the microcapillary, making the viscosity coefficients of both fluids and the electrical conductivity of the inner fluid temperature dependent. The above makes the variables of the flow field in both fluids, velocity, pressure, temperature and electric fields, coupled. An additional complexity of the mathematical model that describes the electroosmotic flow is the nonlinear character due to the rheological behavior of the surrounding fluid. Therefore, based on the lubrication theory approximation, the governing equations are nondimensionalized and simplified, and an asymptotic solution is determined using a regular perturbation technique by considering that the perturbation parameter is associated with changes in the viscosity by temperature effects. The principal results showed that the parameters that notably influence the flow field are the power-law index, an electrokinetic parameter (the ratio between the radius of the microchannel and the Debye length) and the competition between the consistency index of the non-Newtonian fluid and the viscosity of the conducting fluid. Additionally, the heat that is dissipated trough the external surface of the microchannel and the sensitivity of the viscosity to temperature changes play important roles, which modify the flow field.

Keywords: Maxwell stress; electroosmotic flow; immiscible fluids; microcapillary; non-isothermal; power-law fluid.

Figure 1

(Color online) Schematic of the electroosmotic flow of two immiscible fluids in a microcapillary: (a) cross-sectional view and (b) side view, depicting both fluids in distinct colors.

Figure 2

Influence of the dimensionless parameter $K_T$ on the dimensionless (a) temperature, (b) pressure, (c) electric field and (d) pressure gradient.

Figure 3

(a) Dimensionless velocity profiles, evaluated at different values of the coordinate $\chi$, and (b) the corresponding pressure gradient along the microcapillary.

Figure 4

Dimensionless velocity profiles for the inner and surrounding fluids as a function of the dimensionless radial coordinates $\eta$ and Z. (a) Effect of the parameter $k_T$; (b) effect of the parameter ${\mathsf{\Gamma }}_a$; (c) effect of the parameter ${\mathsf{\Gamma }}_{\sigma }$.

Figure 5

Influence of the viscosity ratio on the dimensionless velocity profiles (a) and dimensionless pressure (b). Volumetric flow rate as a function of the viscosity ratio (c) and the effect of the thermal conductivity ratio between the surrounding and inner fluids on the dimensionless velocity profiles (d).

Figure 6

Behavior of the electroosmotic flow with respect to the power-law index n: (a) dimensionless velocity profiles, (b) dimensionless flow rate, (c) dimensionless temperature and (d) dimensionless pressure.

Figure 7

Behavior of the electroosmotic flow: (a) dimensionless velocity profile, evaluated at $\chi =0.5$, and (b) dimensionless pressure along the microcapillary.

Figure 8

Volumetric flow rates for the inner and surrounding fluids: (a) effect of the parameter $k_T$; (b) effect of the parameter $\overline{\kappa }$; (c) effect of the parameter ${\mathsf{\Gamma }}_{\sigma }$.