The Parametric Study of Electroosmotically Driven Flow of Power-Law Fluid in a Cylindrical Microcapillary at High Zeta Potential

Abstract

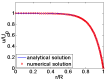
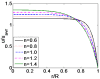
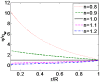
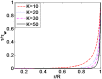
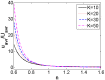
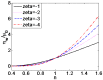
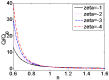
Due to the increasingly wide application of electroosmotic flow in micromachines, this paper investigates the electroosmotic flow of the power-law fluid under high zeta potential in a cylindrical microcapillary for different dimensionless parameters. The electric potential distribution inside a cylindrical microcapillary is presented by the complete Poisson-Boltzmann equation applicable to an arbitrary zeta potential. By solving the Cauchy momentum equation of power-law fluids, the velocity profile, the volumetric flow rate, the average velocity, the shear stress distribution and dynamic viscosity of electroosmotic flow of power-law fluids in a cylindrical microcapillary are studied for different low/high zeta potential, flow behavior index, dimensionless electrokinetic width. The velocity profile gradually changes from parabolic to plug-like shape as the flow behavior index decreases or as the dimensionless electrokinetic width increases. For shear thinning fluids, the viscosity is greater in the center of the microchannel than that near the channel wall, the reverse is true for the shear thickening fluids. Greater volumetric rate and average velocity can be achieved by enhancing the dimensionless electrokinetic width, flow behavior index and zeta potential. It is noted that zeta potential and flow behavior index are important parameters to adjust electroosmotic flow behavior in a cylindrical microcapillary.

Keywords: electroosmotic flow; flow behavior index; high zeta potential; power-law fluids; volumetric flow rate.

Figure 1

Schematic of the cylindrical microcapillary and the coordinate system used for modeling.

Figure 2

The comparison of the analytical solution with the numerical solution (n = 1 and $\overline{\xi }$ = −1).

Figure 3

The comparison of the velocity profiles for different zeta potential (n = 1, K = 10), where the reference velocity is defined as U₀ = ($\epsilon {\epsilon }_0$/${\mu }_0$)·E·($k_b$T/e).

Figure 4

The comparison of the dimensionless velocity profiles generalized with the respective dimensionless average velocity for various flow behavior index n (K = 10, $\overline{\xi }$ = −4).

Figure 5

The comparison of dimensionless dynamic viscosity distributions generalized with the respective magnitude of dynamic viscosity at the channel wall ${\eta }_w$ for various values of flow behavior index n (K = 10, $\overline{\xi }$ = −4).

Figure 6

The comparison of the velocity profiles for various width ratio K under the situation of various flow behavior index n ($\overline{\xi }$ = −4): (a) n = 0.8; (b) n = 1.2; (c) n = 1.

Figure 7

The corresponding changes of dimensionless shear stress distribution generalized with the magnitude of shear stress at the channel wall ${\tau }_w$ for various width ratio K ($\overline{\xi }$ = −4).

Figure 8

The variation of dimensionless average velocity generalized with the average velocity of Newtonian fluid (n = 1) with flow behavior index n under the situation of different width ratio K ($\overline{\xi }$ = −4).

Figure 9

The variation of dimensionless dynamic viscosity at the channel wall generalized with the viscosity of Newtonian fluid ${\mu }_0$ with flow behavior index n under the situation of different dimensionless zeta potential $\overline{\xi }$ (K = 10).

Figure 10

The variation of dimensionless volumetric flow rate generalized with the volumetric flow rate of Newtonian fluid (n = 1) with flow behavior index n under the situation of different zeta potential $\overline{\xi }$ (K = 50).