Estimates of the Heritability of Human Longevity Are Substantially Inflated due to Assortative Mating
- PMID: 30401766
- PMCID: PMC6218226
- DOI: 10.1534/genetics.118.301613
Estimates of the Heritability of Human Longevity Are Substantially Inflated due to Assortative Mating
Abstract
Human life span is a phenotype that integrates many aspects of health and environment into a single ultimate quantity: the elapsed time between birth and death. Though it is widely believed that long life runs in families for genetic reasons, estimates of life span "heritability" are consistently low (∼15-30%). Here, we used pedigree data from Ancestry public trees, including hundreds of millions of historical persons, to estimate the heritability of human longevity. Although "nominal heritability" estimates based on correlations among genetic relatives agreed with prior literature, the majority of that correlation was also captured by correlations among nongenetic (in-law) relatives, suggestive of highly assortative mating around life span-influencing factors (genetic and/or environmental). We used structural equation modeling to account for assortative mating, and concluded that the true heritability of human longevity for birth cohorts across the 1800s and early 1900s was well below 10%, and that it has been generally overestimated due to the effect of assortative mating.
Keywords: assortative mating; heritability; human; life span.
Copyright © 2018 by the Genetics Society of America.
Figures

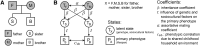
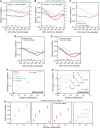


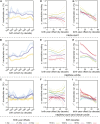
References
-
- Ancestry.com and Board for Certification of Genealogists , 2014. Genealogy Standards. Ancestry.com, Provo, UT.
-
- Björklund A., Eriksson T., Jäntti M., Raaum O., Österbacka E., 2002. Brother correlations in earnings in Denmark, Finland, Norway and Sweden compared to the United States. J. Popul. Econ. 15: 757–772. 10.1007/s001480100095 - DOI
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

